2022-2023学年安徽省蚌埠市蚌山区八年级（下）月考数学试卷（5月份）

一、选择题（本大题共10小题，每小题4分，共40分）

• 1．九边形的内角和等于（　　）

  A．1080°

  B．1260°

  C．1440°

  D．1620°
  组卷：142引用：3难度：0.9

  解析

• 2．下列运算正确的是（　　）

  A． （ - 3 ） 2 = - 3

  B． （ - 5 ） 2 = - 5

  C． 3 + 3 = 2 6

  D． 6 ÷ 3 = 2
  组卷：15引用：2难度：0.7

  解析

• 3．已知a,b,c是△ABC的三条边，满足下列条件仍不能判断△ABC是直角三角形的是（　　）

  A．b2-c2=a2	B．a：b：c=5：12：13
  C．∠A：∠B：∠C=3：4：5	D．∠C=∠A-∠B
  组卷：78引用：2难度：0.6

  解析

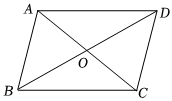• 4．如图，四边形ABCD的对角线AC与BD相交于点O，OA=OC，OB=OD，添加下列条件仍不能判断四边形ABCD是菱形的是（　　）
  ​

  A．BD平分∠ABC	B．AC=BD
  C．AC⊥BD	D．AB2=OA2+OB2
  组卷：163引用：2难度：0.6

  解析

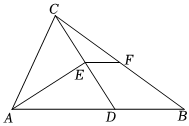• 5．如图，在△ABC中，D是AB上一点，∠ACD=∠ADC，AE平分∠CAD交CD于点E，点F是BC的中点，若AB=12，AC=7，则EF的长为（　　）

  A．5

  B．4

  C．2.5

  D．2
  组卷：16引用：1难度：0.7

  解析

• 6．下面边长相等的正多边形能用来作平面镶嵌的是（　　）

  A．3个等边三角形和2个正方形

  B．2个正五边形和2个等边三角形

  C．1个正方形和2个正六边形

  D．1个正六边形和5个等边三角形
  组卷：100引用：4难度：0.5

  解析

• 7．已知直角三角形的两边长分别为3和5，则第三边长是（　　）

  A．4

  B． 34

  C．4或 34

  D．7
  组卷：705引用：8难度：0.5

  解析

七、（本题满分12分）

• 22．为庆祝“五四青年节”，某校计划购买A与B两种墙贴共400张来布置校园．已知A墙贴的售价是每张16元，B墙贴的售价是每张20元，共花费7040元．
  （1）求计划购买A，B墙贴各多少张？
  （2）为了节省费用，学校采购人员最终决定在网上购买，A墙贴每张售价减少了

  3

  8

  ，B墙贴每张售价便宜了m元，实际购买B墙贴的数量比原计划增加了4m张，总数量不变，总费用比原计划减少了2140元，求m的值．
  组卷：163引用：2难度：0.6

  解析

八、（本题满分14分）

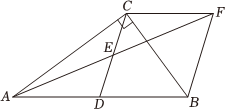• 23．如图，△ABC中，∠ACB=90°，CD是斜边AB上的中线，点E是CD的中点，过点C作CF∥AB交AE的延长线于点F，连接BF．
  （1）求证：CF=CD；
  （2）①当线段AC、BC满足什么数量关系时，四边形CDBF是正方形，并说明理由；
  ②已知

  AC

  =

  2

  5

  ，BC：AB=2：3，求四边形CDBF的面积．
  组卷：61引用：3难度：0.3

  解析