2022-2023学年安徽省安庆市宿松县八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，满分30分。每小题只有一个选项符合题意，请将正确选项的代号填入相应的括号内）

• 1．下列二次根式中，是最简二次根式是（　　）

  A． 0 . 5

  B． 16

  C． 7

  D． 1 3
  组卷：14引用：1难度：0.7

  解析

• 2．以下列数据为长度的线段中，可以构成直角三角形的是（　　）

  A．1，2，3

  B．2，3，4

  C．1， 2 ， 3

  D． 2 ，3，5
  组卷：1290引用：19难度：0.8

  解析

• 3．一元二次方程（x-2）（x-3）=1化为一般形式后，常数项为（　　）

  A．-6

  B．6

  C．-5

  D．5
  组卷：671引用：2难度：0.7

  解析

• 4．估计

  32

  ×

  1

  2

  +

  20

  的运算结果应在（　　）

  A．6到7之间

  B．7到8之间

  C．8到9之间

  D．9到10之间
  组卷：3667引用：124难度：0.9

  解析

• 5．若关于x的一元二次方程（a-1）x²-2x+2=0有实数根，则整数a的最大值为（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：3020引用：68难度：0.7

  解析

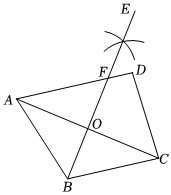• 6．如​图，在四边形ABCD中，AD∥BC，∠D=90°，AD=8，BC=5，分别以点A，C为圆心，大于

  1

  2

  AC长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（　　）

  A．4

  B．4 2

  C．5

  D．5 2
  组卷：30引用：1难度：0.5

  解析

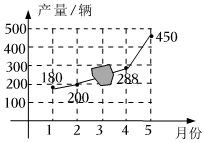• 7．某厂家2022年1～5月份的自行车产量统计图如图所示，3月份自行车产量不小心被墨汁覆盖．若2月份到4月份该厂家自行车产量的月增长率都相同，则3月份自行车产量为（　　）

  A．218辆

  B．240辆

  C．256辆

  D．272辆
  组卷：465引用：5难度：0.5

  解析

三、解答题（本大题共9小题，满分74分）

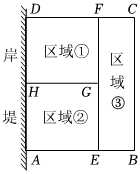• 22．为了节省材料，某水产养殖户利用水库的一段平直的岸堤（岸堤长20米）为一边，用总长为80米的围网，在水库中围成了如图所示的①②③三块不同的矩形区域用于不同水产的养殖，且这三块矩形区域的面积相等．
  （1）设BE的长度为x米，则AE=

  米，BC=

  米；（用含x的代数式表示）；
  （2）当矩形ABCD面积为288米²时，求BC的长度；
  （3）矩形ABCD的面积能不能等于360米²，为什么？
  组卷：334引用：1难度：0.5

  解析

• 23．【问题提出】
  （1）如图1，在△ABC中，可知AC

  AB+BC；（填“＞”“＜”或“=”）
  【问题探究】
  （2）如图2，在菱形ABCD中，∠C=60°，E是对角线BD上一点，延长AB至点F，使得BF=DE，连接AE，EF．求证：AE=EF；
  【问题解决】
  （3）如图3，某市一湿地公园内有一块形如正方形ABCD的观光区，已知AB=6km.为了进一步提升服务休闲功能，满足市民游园和健身需求，现要沿DE，DF分别修建步行景观道，其中，点E，F分别在边BC和对角线AC上，AF=BE．为了节省成本，要使所修的步行景观道之和最短，即DE+DF的值最小，试求DE+DF的最小值．（路面宽度忽略不计）
  
  组卷：198引用：5难度：0.5

  解析