2023-2024学年江苏省扬州市江都区八校联考八年级（上）月考数学试卷（10月份）
发布：2024/9/1 6:0:10
一．选择题（每题3分，共计24分.）
-
1．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史，下列由黑白棋子摆成的图案是轴对称图形的是（ ）
组卷：3621引用：89难度：0.9 -
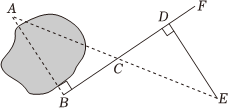2．如图，要测量池塘两岸相对的两点A，B的距离，小明在池塘外取AB的垂线BF上的点C，D，使BC=CD，再画出BF的垂线DE，使E与A，C在一条直线上，这时测得DE的长就是AB的长，依据是（ ）组卷：4013引用：38难度：0.5 -
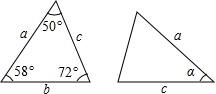3．已知图中的两个三角形全等，则∠α度数是（ ）组卷：2671引用：33难度：0.9 -
4．如图，已知∠DAB=∠CAB，添加下列条件不能判定△DAB≌△CAB的是（ ）组卷：907引用：22难度：0.7 -
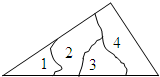5．如图，一块三角形玻璃碎成了4块，现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃，那么最省事的办法是带（ ）去．组卷：2751引用：20难度：0.7 -
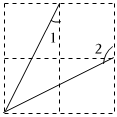6．如图，在由4个相同的小正方形拼成的网格中，∠2-∠1=（ ）组卷：1310引用：16难度：0.6 -
7．小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°．爸爸在C处接住小丽时，小丽距离地面的高度是（ ）
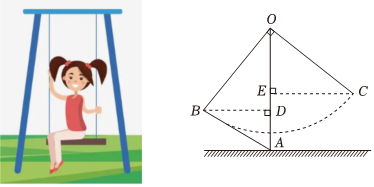组卷：4203引用：30难度：0.5 -
8．如图是一纸条的示意图，第1次对折，使A，B两点重合后再打开，折痕为l1；第2次对折，使A，C两点重合后再打开，折痕为l2；第3次对折，使B，D两点重合后再打开，折痕为l3．已知CE=2cm,则纸条原长为（ ）cm.
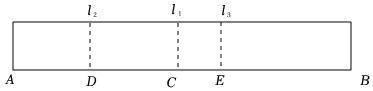组卷：397引用：3难度：0.3
二．填空题（每空3分，共30分．）
-
9．四个图形分别是正三角形、等腰梯形、长方形、正五边形，它们全部是轴对称图形，其中对称轴的条数最少的图形是 ．
组卷：365引用：16难度：0.7
三．解答题（共96分．）
-
27．【阅读理解】
课外兴趣小组活动时，老师提出了如下问题：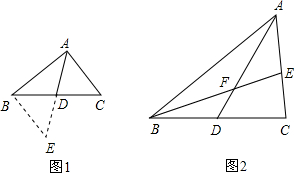
如图1，△ABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请根据小明的方法思考：
（1）由已知和作图能得到△ADC≌△EDB的理由是．
A．SSS B．SAS C．AAS D．HL
（2）求得AD的取值范围是．
A．6＜AD＜8 B．6≤AD≤8 C．1＜AD＜7 D．1≤AD≤7
【感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】
（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．求证：AC=BF．组卷：11748引用：19难度：0.1 -
28．（1）如图①，在四边形ABCD中，AB=AD，∠B=∠D=90°，E，F分别是边BC，CD上的点，且∠EAF=
∠BAD．请直接写出线段EF，BE，FD之间的数量关系：；12
（2）如图②，在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是边BC，CD上的点，且∠EAF=∠BAD，（1）中的结论是否仍然成立？请写出证明过程；12
（3）在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是边BC，CD所在直线上的点，且∠EAF=∠BAD．请直接写出线段EF，BE，FD之间的数量关系：．12
组卷：14661引用：20难度：0.3
