2023-2024学年辽宁省鞍山市千山区九年级(上)期中数学试卷
发布:2024/9/30 12:0:1
一、选择题(每小题2分,共16分)
-
1.用配方法解一元二次方程x2-6x+8=0时,则方程变形正确的是( )
组卷:248引用:24难度:0.7 -
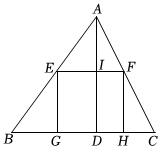 2.如图,已知△ABC是一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是( )mm.组卷:506引用:3难度:0.6
2.如图,已知△ABC是一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是( )mm.组卷:506引用:3难度:0.6 -
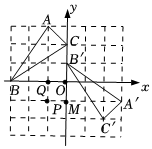 3.如图,在正方形网格中,△ABC绕某点旋转一定的角度得到△A′B′C′,则旋转中心是点( )组卷:1078引用:13难度:0.8
3.如图,在正方形网格中,△ABC绕某点旋转一定的角度得到△A′B′C′,则旋转中心是点( )组卷:1078引用:13难度:0.8 -
4.二次函数y=2x2-bx-1的图象经过点(3,y0)和(9,y0),则b的值为( )
组卷:305引用:6难度:0.6 -
5.已知关于x的方程(m-1)x2-4x+1=0有两个实数根,则m的取值范围是( )
组卷:140引用:4难度:0.7 -
6.已知点P(2a+1,a-1)关于原点对称的点在第一象限,则a的取值范围是( )
组卷:1035引用:12难度:0.8 -
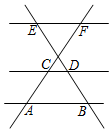 7.如图,已知AB∥CD∥EF,CF:AF=3:5,DE=6,BE的长为( )组卷:749引用:8难度:0.7
7.如图,已知AB∥CD∥EF,CF:AF=3:5,DE=6,BE的长为( )组卷:749引用:8难度:0.7 -
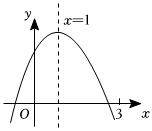 8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a-b+c>0;⑤若+bx1=ax21+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )ax22组卷:6508引用:26难度:0.2
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a-b+c>0;⑤若+bx1=ax21+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )ax22组卷:6508引用:26难度:0.2
三、解答题(共88分)
-
25.已知,在正方形ABCD中,对角线AC与BD相交于点O.
(1)如图1,将线段CO绕点C顺时针旋转90°得到CE,连接BE交CO于点F,求证:BF=EF.
(2)如图2,若CD=4,点P是CD边上的点,且CP=1,连接OP,将线段OP绕点P顺时针旋转90°得到PH,连接BH交CO于点G.求OG的长.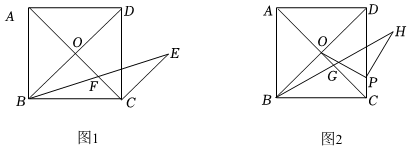 组卷:363引用:3难度:0.1
组卷:363引用:3难度:0.1 -
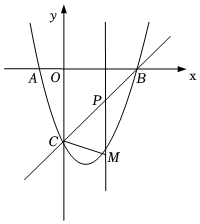 26.如图,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.
26.如图,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.
(1)求抛物线的解析式;
(2)如图,若点P是线段BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,当△PCM和△ABC相似时,求此时点P的坐标;
(3)若点P是直线BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,将△PCM沿CM对折,如果点P的对应点N恰好落在y轴上,求此时点P的坐标;组卷:2379引用:11难度:0.4


