2020-2021学年浙江省宁波大学附属学校八年级（上）段考数学试卷（10月份）

一、选择题（每小题3分，共30分）

• 1．下列图标中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：27引用：3难度：0.8

  解析

• 2．在平面直角坐标系中，点（-1，2）在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：2732引用：75难度：0.9

  解析

• 3．下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（　　）

  A．1，2，1

  B．1，2，3

  C．1，2，2

  D．1，2，4
  组卷：233引用：83难度：0.9

  解析

• 4．下列能断定△ABC为等腰三角形的是（　　）

  A．∠A=30°，∠B=60°	B．∠A+∠B=∠C
  C．∠A=55°，∠B=70°	D．∠A：∠B=1：2
  组卷：115引用：4难度：0.7

  解析

• 5．下列说法正确的是（　　）

  A．周长相等的两个三角形全等

  B．面积相等的两个三角形全等

  C．完全重合的两个三角形全等

  D．所有的等边三角形全等
  组卷：166引用：12难度：0.9

  解析

• 6．已知a＞b,则下列变形正确的是（　　）

  A．a+2＜b+2

  B．a-2＜b-2

  C．2a＜2b

  D．-a＜-b
  组卷：613引用：5难度：0.7

  解析

• 7．下列选项中，可以用来说明“若a＞b,则|a|＞|b|”是假命题的反例是（　　）

  A．a=2，b=-3

  B．a=3，b=2

  C．a=2，b=3

  D．a=-3，b=2
  组卷：238引用：12难度：0.6

  解析

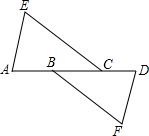• 8．如图，AE∥DF，AE=DF，则添加下列条件还不能使△EAC≌△FDB的为（　　）

  A．AB=CD

  B．CE∥BF

  C．∠E=∠F

  D．CE=BF
  组卷：212引用：4难度：0.7

  解析

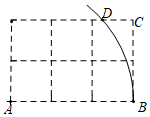• 9．如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（　　）

  A． 5

  B．0.8

  C．3- 5

  D． 13
  组卷：7161引用：41难度：0.5

  解析

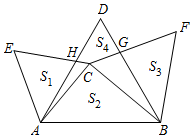• 10．如图，在Rt△ABC中，∠ACB=90°，以AB，AC，BC为边作等边△ABD，等边△ACE，等边△CBF．设△AEH的面积为S₁，△ABC的面积为S₂，△BFG的面积为S₃，四边形DHCG的面积为S₄，则下列结论正确的是（　　）

  A．S2=S1+S3+S4	B．S1+S2=S3+S4
  C．S1+S4=S2+S3	D．S1+S3=S2+S4
  组卷：1830引用：7难度：0.6

  解析

三、解答题（每小题10分，共20分）

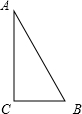• 30．如图，△ABC中，∠C=90°，AB=5cm,BC=3cm,若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm,设出发的时间为t秒．
  （1）出发2秒后，求△ABP的周长．
  （2）问t为何值时，△BCP为等腰三角形？
  （3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm,若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
  组卷：16280引用：40难度：0.1

  解析

• 31．已知：△ABC和△ADE是两个不全等的等腰直角三角形，其中BA=BC，DA=DE，连接EC，取EC的中点M，连接BM和DM．
  （1）如图1，如果点D、E分别在边AC、AB上，那么BM、DM的数量关系与位置关系是

   

  ；
  （2）将图1中的△ADE绕点A旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．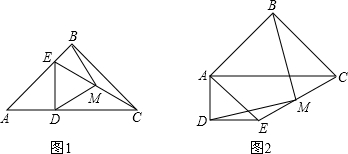
  
  组卷：825引用：3难度：0.5

  解析