当前位置：试卷中心 > 试卷详情

2023-2024学年广东省湛江市雷州市八年级（上）第一次月考数学试卷

发布：2024/9/23 6:0:8

1．下列长度的三条线段能组成三角形的是（　　）
A．1，2，3 B．2，3，5 C．3，4，8 D．5，6，10
组卷：89引用：6难度：0.9
解析
2．以下生活现象不是利用三角形稳定性的是（　　）
A． B． C． D．
组卷：333引用：19难度：0.5
解析
3．若一个多边形的内角和为540°，则该多边形为（　　）边形．
A．四 B．五 C．六 D．七
组卷：409引用：10难度：0.8
解析
4．张老师让同学们作三角形BC边上的高，你认为正确的是（　　）
A． B． C． D．
组卷：679引用：8难度：0.7
解析
5．一等腰三角形的两边长分别为4和8，则这个等腰三角形的周长为（　　）
A．16 B．20 C．18 D．16或20
组卷：629引用：17难度：0.9
解析
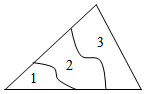6．如图，一块三角形的玻璃碎成3块（图中所标1、2、3），小华带第3块碎片去玻璃店，购买形状相同、大小相等的新玻璃，这是利用三角形全等中的（　　）
A．SSS B．ASA C．AAS D．SAS
组卷：867引用：11难度：0.7
解析
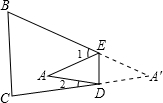7．如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，如果∠1=40°，∠2=30°，那么∠A=（　　）
A．40° B．30° C．70° D．35°
组卷：980引用：7难度：0.6
解析
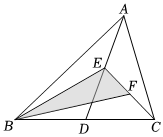8．如图，在△ABC中，已知点E、F分别为中线AD、中线CE的中点，且S_△ABC=20，则S_阴影=（　　）
A．10 B．5 C．4 D．
5
2
组卷：104引用：1难度：0.5
解析

24．如图，在Rt△ABC与Rt△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE．BD与CE相交于点F．
（1）求证：BD=EC；
（2）求证：BD⊥CE．
组卷：16引用：1难度：0.7
解析
25．如图，AB=12cm,AC⊥AB，BD⊥AB，AC=BD=9cm,点P在线段AB上以3cm/s的速度，由A向B运动，同时点Q在线段BD上由B向D运动．
（1）若点Q的运动速度与点P的运动速度相等，当运动时间t=1（s），△ACP与△BPQ是否全等？说明理由，并直接判断此时线段PC和线段PQ的位置关系；
（2）将“AC⊥AB，BD⊥AB”为改“∠CAB=∠DBA”，其他条件不变．若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使△ACP与△BPQ全等．
（3）在图2的基础上延长AC，BD交于点E，使C，D分别是AE，BD中点，若点Q以（2）中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿△ABE三边运动，求出经过多长时间点P与点Q第一次相遇．
组卷：260引用：7难度：0.2
解析