2022-2023学年江西省新余三中八年级（上）第二次质检数学试卷

一、单选题（共6题，每题3分，共18分）

• 1．图形是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：2引用：1难度：0.9

  解析

• 2．在下列长度的四组线段中，不能组成三角形的是（　　）

  A．3，4，6

  B．5，6，10

  C．3，5，7

  D．4，6，10
  组卷：145引用：7难度：0.7

  解析

• 3．若点A（-4，m-3），B（2n,1）关于x轴对称，则m+n=（　　）

  A．0

  B．2

  C．4

  D．6
  组卷：737引用：4难度：0.7

  解析

• 4．等腰三角形两边长为3和6，则周长为（　　）

  A．12

  B．15

  C．12或15

  D．无法确定
  组卷：171引用：15难度：0.9

  解析

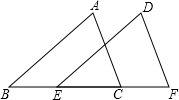• 5．如图，已知点B、E、C、F在同一直线上，且BE=CF，∠ABC=∠DEF，那么添加一个条件后．仍无法判定△ABC≌△DEF的是（　　）

  A．AC=DF

  B．AB=DE

  C．AC∥DF

  D．∠A=∠D
  组卷：511引用：13难度：0.9

  解析

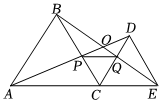• 6．如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．下列结论：①AD=BE；②AP=BQ；③PQ∥AE；④∠AOB=60°；⑤DE=DP；⑥连接OC，OC平分∠AOE；⑦△CPQ为等边三角形．其中正确的有（　　）

  A．4个

  B．5个

  C．6个

  D．7个
  组卷：232引用：6难度：0.5

  解析

二、填空题（共6题，每题3分，共18分）

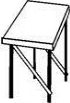• 7．如图，李叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是

  ．
  组卷：3386引用：58难度：0.5

  解析

五、解答题（每小题9分，共18分）

• 22．通过对如图数学模型的研究学习，解决下列问题：
  [模型呈现]
  如图1，∠BAD=90°，AB=AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D．又∠ACB=∠AED=90°，可以推理得到△ABC≌△DAE．进而得到AC=

  ，BC=AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；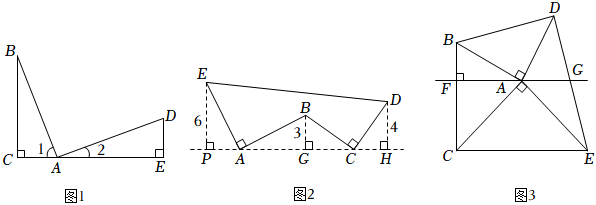
  
  [模型应用]
  如图2，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积为

  ．
  A.50
  B.62
  C.65
  D.68
  [深入探究]
  如图3，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；
  组卷：1803引用：11难度：0.1

  解析

六、解答题（共12分）

• 23．在Rt△ABC中，∠CAB=90°，AB=AC，点O是BC的中点，点P是射线CB上的一个动点（点P不与点C、O、B重合），过点C作CE⊥AP于点E，过点B作BF⊥AP于点F，连接EO，OF．
  （问题探究）
  如图1，当P点在线段CO上运动时，延长EO交BF于点G．
  （1）求证：△AEC≌△BFA；
  （2）BG与AF的数量关系为：

  （直接写结论，不需说明理由）；
  （拓展延伸）
  （3）①如图2，当P点在线段OB上运动，EO的延长线与BF的延长线交于点G，∠OFE的大小是否变化？若不变，求出∠OFE的度数；若变化，请说明理由；
  ②当P点在射线OB上运动时，若AE=2，CE=5，直接写出△OEF的面积，不需证明．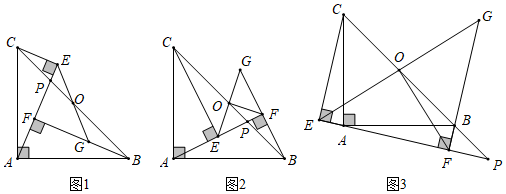
  
  组卷：491引用：6难度：0.1

  解析