人教新版八年级上册《第14章 整式的乘法与因式分解》2023年单元测试卷（9）

一、选择题

• 1．下列计算中正确的是（　　）

  A．a3•a2=a6	B．（a2b）3=a6b
  C．a3+a2=a5	D．（-x）5•（-x）3=x8
  组卷：114引用：2难度：0.9

  解析

• 2．计算（x-1）（x²+x+1）的结果应是（　　）

  A．x3-1	B．x3+1
  C．x3-2x-1	D．x3-2x2+2x-1
  组卷：138引用：2难度：0.7

  解析

• 3．下列各多项式中不能用公式法分解的是（　　）

  A．x2-（-y）2

  B．a2-ab+ 1 4 b2

  C．x2-2x-1

  D．25-10x+x2
  组卷：68引用：2难度：0.7

  解析

• 4．若x^m÷x²ⁿ⁺¹=x,则m与n的关系是（　　）

  A．m=2n+1

  B．m=-2n-1

  C．m-2n=2

  D．m-2n=-2
  组卷：1643引用：8难度：0.9

  解析

• 5．若2^m=5，4ⁿ=3，则4^3n-m的值是（　　）

  A． 9 10

  B． 27 25

  C．2

  D．4
  组卷：2158引用：8难度：0.7

  解析

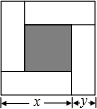• 6．如图，大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同长方形的两边长（x＞y），给出以下关系式：①x+y=m；②x-y=n；③xy=

  m

  2

  -

  n

  2

  4

  ．其中正确的关系式的个数有（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：1306引用：3难度：0.7

  解析

• 7．下列各式中，计算正确的是（　　）

  A．（-5an+1b）•（-2a）=10an+1b

  B．（-4a2b）•（-a2b2）• 1 2 b 3 c = 2 a 4 b 6 c

  C．（-3xy）•（-x2z）•6xy2=3x3y3z

  D． （ 2 a n b 3 ） （ - 1 6 a b n - 1 ） = 1 3 a n + 1 b 3 n - 1
  组卷：1525引用：4难度：0.7

  解析

• 8．观察下列等式：9-1=8，16-4=12，25-9=16，36-16=20，…设n表示正整数，下面符合上述规律的等式是（　　）

  A．（n+2）2-n2=4（n+1）	B．（n+1）2-（n-1）2=4n
  C．（n+2）2-n2=4n+1	D．（n+2）2-n2=2（n+1）
  组卷：211引用：7难度：0.9

  解析

• 9．已知（m-n）²=32，（m+n）²=4000，则m²+n²的值为（　　）

  A．2014

  B．2015

  C．2016

  D．4032
  组卷：1052引用：8难度：0.7

  解析

三、解答题

• 27．阅读理解并填空：
  （1）为了求代数式x²+2x+3的值，我们必须知道x的值．
  若x=1，则这个代数式的值为

  ，
  若x=2，则这个代数式的值为

  ，
  …可见，这个代数式的值因x的取值不同而变化，尽管如此，我们还是有办法来考虑这个代数式的值的范围．
  （2）把一个多项式进行部分因式分解可以解决求代数式的最大（或最小）值问题．
  例如x²+2x+3=x²+2x+1+2=（x+1）²+2，因为（x+1）²是非负数，所以这个代数式的最小值是

  ，此时相应的x的值是

  ．
  （3）求代数式x²-12x+35的最小值，并写出相应的x的值．
  （4）求代数式-x²-6x+12的最大值，并写出相应的x的值．
  组卷：884引用：3难度：0.3

  解析

• 28．已知a,b,c是△ABC的三边，试判断（a²+b²+c²）²与4a²b²的大小．
  组卷：53引用：2难度：0.7

  解析