2023-2024学年北京市东城区文汇中学八年级（上）期中数学试卷

一、选择题（每小题只有一个选项符合题意，每题3分，共30分）

• 1．《国语•楚语》记载：“夫美者，上下、内外、大小、远近皆无害焉，故曰美”．这一记载充分表明传统美的本质特征在于对称和谐．中国建筑布局一般都是采用均衡对称的方式建造，更具脱俗的美感和生命力．下列建筑物的简图中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：141引用：9难度：0.8

  解析

• 2．正五边形的外角和为（　　）

  A．180°

  B．360°

  C．540°

  D．720°
  组卷：2275引用：57难度：0.8

  解析

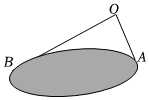• 3．为估计池塘两岸 A、B间的距离，如图，小明在池塘一侧选取了点O，测得OA=8m,OB=15m,那么 A、B间的距离不可能是（　　）

  A．7 m

  B．13 m

  C．14m

  D．15m
  组卷：423引用：5难度：0.7

  解析

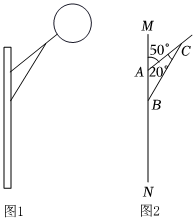• 4．图1是一路灯的实物图，图2是该路灯的平面示意图，∠MAC=50°，∠ACB=20°，则图2中∠CBA的度数为（　　）

  A．15°

  B．20°

  C．30°

  D．50°
  组卷：595引用：8难度：0.7

  解析

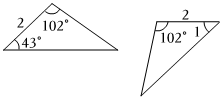• 5．如图的两个三角形是全等三角形，其中角和边的大小如图所示，那么∠1的度数是（　　）

  A．43°

  B．35°

  C．55°

  D．47°
  组卷：70引用：3难度：0.7

  解析

• 6．用直角三角板，作△ABC的高，下列作法正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：1108引用：48难度：0.9

  解析

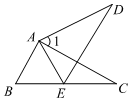• 7．如图，△ABC≌△AED，点E在线段BC上，∠1=56°，则∠AED的大小为（　　）

  A．34°

  B．56°

  C．62°

  D．68°
  组卷：592引用：9难度：0.6

  解析

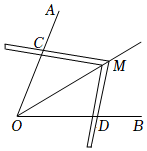• 8．工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别在取OC=OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线，这里构造全等三角形的依据是（　　）

  A．SSS

  B．ASA

  C．AAS

  D．SAS
  组卷：2972引用：33难度：0.7

  解析

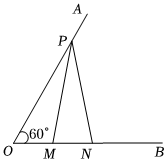• 9．如图所示，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=1，则OM的长为（　　）

  A．4

  B．4.5

  C．5

  D．5.5
  组卷：494引用：5难度：0.7

  解析

三、解答题（共54分，19-22题每题5分，23-25题每题6分，26-27题每题8分）

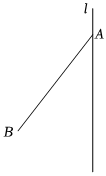• 26．已知：线段AB及过点A的直线l.如果线段AC与线段AB关于直线l对称，连接BC交直线l于点D，以AC为边作等边△ACE，使得点E在AC的下方，作射线BE交直线l于点F，连结CF．
  （1）根据题意补全图形；
  （2）如图，如果∠BAD=α（30°＜α＜60°），
  ①∠ABE=

  ；（用含有α代数式表示）
  ②用等式表示线段FA，FE与FC的数量关系，并证明．
  组卷：524引用：6难度：0.4

  解析

• 27．在平面中，对于点M，N，P，若∠MPN=90°，且PM=PN，则称点P是点M和点N的“垂等点”．
  在平面直角坐标系xOy中，
  （1）已知点M（-3，2），点N（1，0），则点P₁（0，3），P₂（-2，-1），P₃（-5，-2）中是点M和点N的“垂等点”的是

  ；
  （2）已知点A（-4，0），B（0，b）（b＞0）．
  ①若在第二象限内存在点C，使得点B是点A和点C的“垂等点”，写出点C的坐标（用含b的式子表示），并说明理由；
  ②当b=4时，点D，点E是线段AO，BO上的动点（点D，点E不与点A，B，O重合）．若点F是点D和点E的“垂等点”，直接写出点F的纵坐标t的取值范围．
  
  组卷：449引用：4难度：0.2

  解析