2020-2021学年河南省安阳五中八年级（上）期中数学试卷

一．选择题（共10小题，每题3分，共30分）

• 1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：3590引用：164难度：0.8

  解析

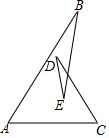• 2．如图，∠A，∠B，∠C，∠D，∠E，五个角的和等于（　　）

  A．90°

  B．180°

  C．360°

  D．540°
  组卷：109引用：2难度：0.8

  解析

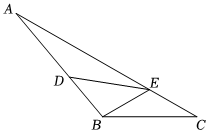• 3．如图，在△ABC中，D，E分别为AB，AC边上的点，DA=DE，DB=BE=EC，若∠ABC=130°，则∠C的度数为（　　）

  A．30°

  B．25°

  C．22.5°

  D．20°
  组卷：113引用：2难度：0.7

  解析

• 4．下列说法中错误的是（　　）

  A．有两个角及它们的夹边对应相等的两个三角形全等

  B．有两个角及其中一个角的对边对应相等的两个三角形全等

  C．有两条边及其中一条边的对角对应相等的两个三角形全等

  D．有两条边及它们的夹角对应相等的两个三角形全等
  组卷：177引用：3难度：0.7

  解析

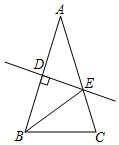• 5．如图，在△ABC中，AB=AC=15cm,AB的垂直平分线交AB于点D，交AC于点E，若△EBC的周长为23cm,则BC的长为（　　）

  A．8cm

  B．7cm

  C．9cm

  D．7.5cm
  组卷：536引用：5难度：0.7

  解析

• 6．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（　　）

  A．40海里

  B．60海里

  C．70海里

  D．80海里
  组卷：2171引用：113难度：0.9

  解析

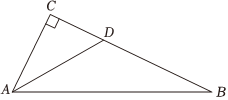• 7．如图所示，在△ABC中，∠C=90°，BC=40，AD是∠BAC的平分线交BC于D，若DC：DB=3：5，则点D到AB的距离是（　　）

  A．40

  B．15

  C．25

  D．20
  组卷：280引用：9难度：0.9

  解析

三．解答题（共8小题，共75分）

• 22．如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．
  （1）求证：△ABC≌△ADE；
  （2）求∠FAE的度数；
  （3）求证：CD=2BF+DE．
  组卷：44367引用：76难度：0.1

  解析

• 23．问题情境：如图1，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
  
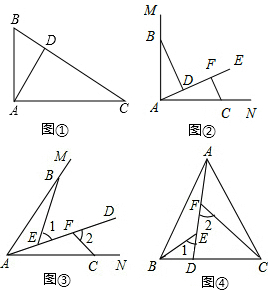
  （1）特例探究：如图2，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；
  （2）归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；
  （3）拓展应用：如图4，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为3，则△ACF与△BDE的面积之和为

  ．
  组卷：573引用：5难度：0.4

  解析