2022-2023学年湖北省随州市曾都区八年级(下)期中数学试卷
发布:2024/6/23 8:0:10
一、选择题(每小题3分,共30分)
-
1.若
有意义,则x的取值范围是( )x-2组卷:809引用:45难度:0.9 -
2.下列各式计算正确的是( )
组卷:4442引用:97难度:0.9 -
3.若a,b为两个有理数,且b=
+4,则a+b的值为( )a2-1+1-a2a+1组卷:462引用:7难度:0.9 -
4.顺次连接矩形的各边中点,所得的四边形一定是( )
组卷:494引用:30难度:0.9 -
5.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
组卷:10489引用:150难度:0.9 -
6.下列命题错误的是( )
组卷:23引用:1难度:0.7 -
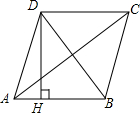 7.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )组卷:14454引用:100难度:0.5
7.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )组卷:14454引用:100难度:0.5 -
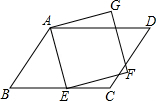 8.如图,在▱ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=45°,∠CEF=15°,则∠D的度数是( )组卷:493引用:6难度:0.5
8.如图,在▱ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=45°,∠CEF=15°,则∠D的度数是( )组卷:493引用:6难度:0.5
三、解答题(共72分)
-
23.(1)观察猜想:如图①所示,在正方形ABCD和正方形CGEF中,点B,C,G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM.易证:DM与FM的数量关系为:;位置关系为:;
(2)数学思考:如图②,当点B,C,F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系.请写出猜想,并给予证明;
(3)拓展延伸:如图③,当点E,B,C在同一条直线上,DM的延长线交CE的延长线于点N;若AB=1,CF=2,请直接写出FM的长.2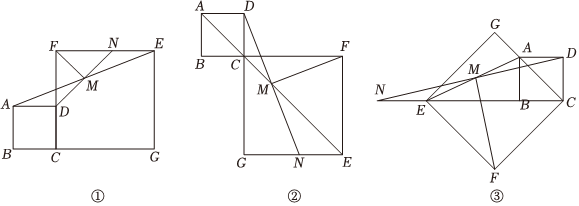 组卷:49引用:1难度:0.1
组卷:49引用:1难度:0.1 -
 24.如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.3
24.如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.3
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.组卷:3780引用:57难度:0.3


