2023-2024学年广东省珠海市香洲区紫荆中学九年级(上)月考数学试卷(10月份)
发布:2024/9/11 2:0:8
一.选择题(每小题3分,共30分)
-
1.m是方程x2+2x-1=0的根,则式子2m2+4m的值为( )
组卷:254引用:3难度:0.5 -
2.若点A(-1,y1),B(2,y2)在抛物线y=-(x+2)2上,则y1,y2的大小关系( )
组卷:388引用:10难度:0.7 -
3.用配方法解一元二次方程x2-6x-5=0,此方程可化为( )
组卷:1317引用:29难度:0.7 -
4.若关于x的方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
组卷:1373引用:25难度:0.9 -
5.二次函数y=2(x-3)2+1的图象的顶点坐标是( )
组卷:965引用:16难度:0.8 -
6.已知m,n为一元二次方程x2+2x-9=0的两个根,则m2+m-n的值为( )
组卷:361引用:6难度:0.7 -
7.若关于x的一元二次方程(m-3)x2+x+m2-9=0的一个根为0,则m的值为( )
组卷:560引用:7难度:0.7 -
8.把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到抛物线( )
组卷:2647引用:61难度:0.9
五.解答题三(每小题12分,共24分)
-
23.已知关于x的方程 mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)若抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,试确定此抛物线的解析式;
(3)若点P(x1,y1)与Q(x1+n,y2)在(2)中抛物线上 (点P、Q不重合),且y1=y2,求代数式4x12+12x1n+5n2+16n+8的值.组卷:304引用:9难度:0.3 -
24.如图①,已知抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.
(1)求抛物线的关系式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.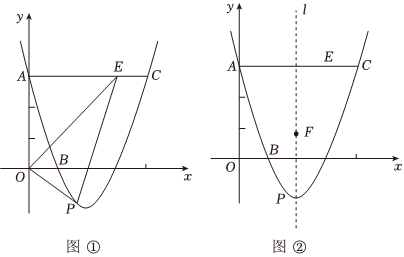 组卷:262引用:2难度:0.5
组卷:262引用:2难度:0.5


