2022-2023学年重庆市合川中学九年级（下）第一次月考数学试卷

一、选择题（本大题10个小题，每题4分，共40分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的，请将答卷上对应的方框涂黑．

• 1．5的相反数是（　　）

  A．-5

  B．- 1 5

  C． 1 5

  D．5
  组卷：136引用：15难度：0.8

  解析

• 2．下列图形既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：66引用：1难度：0.9

  解析

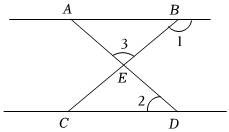• 3．已知AD与BC相交于点E，且AB∥CD，∠1=140°，∠2=40°，则∠3等于多少度（　　）

  A．80°

  B．90°

  C．100°

  D．110°
  组卷：128引用：1难度：0.7

  解析

• 4．寒假里小林去海南旅游，某日他观测了海滨浴场从早上8点到晚上8点的水位变化情况，记录结果如图所示．则下列说法正确的是（　　）

  A．8时水位最低

  B．8时至12时，水位最高为7米

  C．8时至14时，水位不断升高

  D．16时至20时，水位不断降低
  组卷：110引用：3难度：0.6

  解析

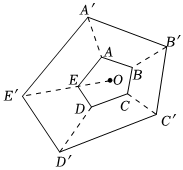• 5．如图，已知五边形ABCDE与五边形A'B'C'D'E'是位似图形，位似中心是O，若五边形ABCDE的面积是2，五边形A'B'C'D'E'的面积是18，则OE：OE'等于（　　）

  A．1：3

  B．1：9

  C．1：2

  D．1：4
  组卷：176引用：4难度：0.5

  解析

• 6．下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有8颗棋子，第③个图形一共有17颗棋子，……，则第⑦个图形中棋子的颗数为（　　）

  A．92

  B．81

  C．73

  D．64
  组卷：229引用：6难度：0.7

  解析

• 7．估计

  5

  （

  7

  +

  1

  5

  ）

  的值应在（　　）

  A．3和4之间

  B．4和5之间

  C．5和6之间

  D．6和7之间
  组卷：42引用：1难度：0.7

  解析

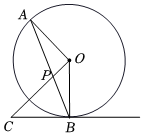• 8．如图，AB是⊙O的弦，PO⊥OA交AB于点P，过点B的切线交OP的延长线于点C，若⊙O的半径为

  2

  5

  ，OP=2，则BC的长为（　　）

  A．2

  B． 2 5

  C．4

  D．5
  组卷：557引用：3难度：0.6

  解析

四、解答题（本大题6个小题，每小题10分，共60分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

• 25．在平面直角坐标系中，抛物线y=ax²+bx+2（a≠0）与x轴的交点为A（-4，0），B（1，0），与y轴交于点C．
  （1）求抛物线的函数表达式；
  （2）如图1，连接AC，P是第二象限内抛物线上一动点，过点P作PG∥y交直线AC于点G，作PR∥x轴交直线AC于点R，求PG+PR最大值以及此时点P的坐标；
  （3）如图2，将抛物线y=ax²+bx+2（a≠0）沿射线AC平移

  5

  个单位，得到新抛物线y′，M为新抛物线对称轴上一点，N为新抛物线上一点，当以P、B、M、N为顶点的四边形是平行四边形时，请直接写出所有符合条件的N点的坐标，并把求其中一个点N的过程写出来．
  
  组卷：486引用：4难度：0.1

  解析

• 26．如图1，△ABC与△EDC为等腰直角三角形，AC=BC=6，DE=DC=2，∠ACB=∠CDE=90°，将△EDC绕着点C旋转．
  （1）如图2，在旋转过程中，当A、C、E三点共线（E在AC延长线上）时，连接BE，过D点作AE的垂线交AE于点G，交BE于点F，求BF的长；
  （2）如图3，在旋转过程中，连接AE、BE，过点D作DF⊥AE于点G，交BE于点F，请写出EF与BF的数量关系并证明．
  （3）如图4，在（2）的条件下，连接CF、AF，当AF最小时，请直接写出△ACF的面积．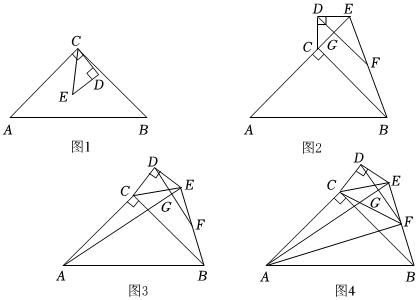
  
  组卷：163引用：1难度：0.1

  解析