当前位置：试卷中心 > 试卷详情

2020-2021学年广西大学附中九年级（上）第二次月考数学试卷

发布：2024/9/6 7:0:8

1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：42引用：2难度：0.7
解析
2．下列方程中，属于一元二次方程的是（　　）
A．2x+y=1 B．ax²+bx+c=0 C．x+
1
x
=3 D．x²一1=0
组卷：65引用：5难度：0.9
解析
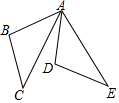3．如图△ABC绕点A旋转至△ADE，则旋转角是（　　）
A．∠BAD B．∠BAC C．∠BAE D．∠CAD
组卷：596引用：15难度：0.8
解析
4．如图，在半径为5cm的⊙O中，圆心O到弦AB的距离为3cm,则弦AB的长是（　　）
A．4cm B．6cm C．8cm D．10cm
组卷：1014引用：14难度：0.9
解析
5．关于x的函数y=（m+2）x
m
2
-
2
是二次函数，则m的值是（　　）
A．2 B．4 C．-2或2 D．-4或4
组卷：3737引用：6难度：0.8
解析
6．下列说法正确的是（　　）
A．圆是轴对称图形，直径是它的对称轴
B．在同圆或等圆中，等弦所对的弧相等
C．三角形的外心到三角形三个顶点距离相等
D．圆的切线垂直于半径
组卷：9引用：2难度：0.5
解析
7．如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB=50°，则∠APB等于（　　）
A．50° B．120° C．100° D．80°
组卷：893引用：6难度：0.7
解析
8．若⊙A的半径为5，圆心A的坐标是（1，2），点P的坐标是（5，2），那么点P的位置为（　　）
A．在⊙A内 B．在⊙A上 C．在⊙A外 D．不能确定
组卷：940引用：8难度：0.8
解析

25．如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，与AC、BC分别交于点M、N，与AB的另一个交点为E．过点N作NF⊥AB，垂足为F．
（1）求证：NF是⊙O的切线；
（2）若NF=2，DF=1，求弦ED的长．
组卷：2354引用：8难度：0.5
解析
26．如图，抛物线y=-
1
2
x²+bx+c过点A（3，2），且与直线y=-x+
7
2
交于B、C两点，点B的坐标为（4，m）．

（1）求抛物线的解析式；
（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；
（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM=45°？若存在，求点Q的坐标；若不存在，请说明理由．
组卷：5748引用：26难度：0.1
解析