2022-2023学年江苏省泰州市姜堰区励才实验学校九年级（上）第二次月考数学试卷

一、选择题（本大题共6小题，每小题3分，共18分）

• 1．已知

  y

  =

  m

  x

  m

  2

  +

  3

  m

  +

  2

  是二次函数，则m的值为（　　）

  A．0或-3

  B．0或3

  C．0

  D．-3
  组卷：393引用：5难度：0.9

  解析

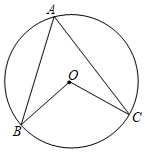• 2．如图，点A，B，C在⊙O上，∠BAC=54°，则∠BOC的度数为（　　）

  A．27°

  B．108°

  C．116°

  D．128°
  组卷：2229引用：42难度：0.9

  解析

• 3．如图，如果∠BAD=∠CAE，那么添加下列一个条件后，仍不能确定△ABC∽△ADE的是（　　）

  A．∠B=∠D

  B． AB AD = DE BC

  C．∠C=∠AED

  D． AB AD = AC AE
  组卷：1492引用：12难度：0.5

  解析

• 4．已知正三角形的边长为12，则这个正三角形外接圆的半径是（　　）

  A．2 3

  B． 3

  C．3 3

  D．4 3
  组卷：585引用：4难度：0.9

  解析

• 5．将抛物线y=4-（x+1）²向右平移1个单位，再向下平移2个单位，所得抛物线必定经过点（　　）

  A．（-2，2）

  B．（-1，1）

  C．（0，6）

  D．（1，-3）
  组卷：304引用：3难度：0.6

  解析

• 6．抛物线y=ax²+bx+c上部分点的横坐标x,纵坐标y的对应值如表，下列结论错误的是（　　）

  x	…	-2	-1	0	1	2	…
  y	…	0	4	6	6	4	…

  A．对称轴是直线x= 1 2

  B．与x轴的交点坐标是（-2，0）（3，0）

  C．抛物线开口向下

  D．ax2+bx+c=4的解是x=±1
  组卷：293引用：3难度：0.7

  解析

二、填空题（本大题共10小题，每小题3分，共30分）

• 7．已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O

  （填“上”“外”或“内”）
  组卷：744引用：32难度：0.9

  解析

• 8．直角三角形的两条直角边分别是5和12，则它的内切圆半径为

  ．
  组卷：1916引用：24难度：0.7

  解析

三、解答题（本大题共10小题，共102分）

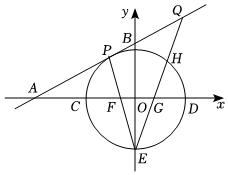• 25．如图，在平面直角坐标系xOy中，直线m：y=

  3

  3

  x+

  2

  3

  3

  与x轴交于点A，与y轴交于点B，点P在直线m上，以点O为圆心，OP为半径的⊙O交x轴于点C、D（点C在点D的左侧），与y轴负半轴交于点E，连接PE，交x轴于点F，且AF=AP．
  （1）判断直线m与⊙O的位置关系，并说明理由；
  （2）求∠PEB的度数；
  （3）若点Q是直线m上位于第一象限内的一个动点，连接EQ交x轴于点G，交⊙O于点H，判断EG•EH是否为定值，若是，求出该定值；若不是，请说明理由．
  组卷：267引用：2难度：0.3

  解析

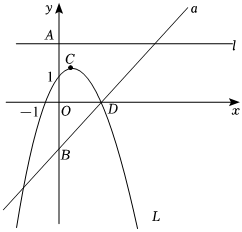• 26．如图，若b是正数，直线l：y=b与y轴交于点A；直线a：y=x-b与y轴交于点B；抛物线L：y=-x²+bx的顶点为C，且L与x轴正半轴的交点为D．
  （1）若AB=8，求b的值，并求此时L的对称轴与a的交点坐标；
  （2）当点C在l下方时，求点C与l距离的最大值；
  （3）设x₀≠0，点（x₀，y₁），（x₀，y₂），（x₀，y₃）分别在l,a和L上，且y₃是y₁，y₂的平均数，求点（x₀，0）与点D间的距离；
  （4）在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b=2019和b=2019.5时“美点”的个数．
  组卷：265引用：2难度：0.2

  解析