2022-2023学年广东省实验中学荔湾学校九年级（上）月考数学试卷（10月份）

一.选择题（每小题3分，滴分30分）

• 1．抛物线y=2（x+9）²-3的顶点坐标是（　　）

  A．（ 9，3）

  B．（9，-3）

  C．（-9，3）

  D．（-9，-3）
  组卷：2980引用：55难度：0.8

  解析

• 2．一元二次方程（x-2）（x+3）=0化为一般形式后，常数项为（　　）

  A．6

  B．-6

  C．1

  D．-1
  组卷：600引用：10难度：0.8

  解析

• 3．一元二次方程（x-1）²+k-3=0的一个根是x=1，则k=（　　）

  A．3

  B．2

  C．-3

  D．-2
  组卷：945引用：11难度：0.8

  解析

• 4．下列关于抛物线y=3（x-1）²+1的说法，正确的是（　　）

  A．开口向下	B．顶点坐标是（-1，1）
  C．有最小值y=1	D．对称轴是直线x=-1
  组卷：963引用：14难度：0.8

  解析

• 5．已知二次函数y=2x²-4x+5，当函数值y随x值的增大而增大时，x的取值范围是（　　）

  A．x＜1

  B．x＞1

  C．x＜2

  D．x＞2
  组卷：4359引用：21难度：0.6

  解析

• 6．用配方法将二次函数y=x²-4x-6化为y=a（x-h）²+k的形式为（　　）

  A．y=（x-2）2-2	B．y=（x-2）2-10
  C．y=（x+2）2-2	D．y=（x+2）2-10
  组卷：1113引用：3难度：0.7

  解析

• 7．小兵在暑假调查了某工厂得知，该工厂2020年全年某产品的产量为234万吨，经该厂的技术人员预计2022年全年该产品的产量为345万吨，设2020年至2022年该产品的预计年平均增长率为x,根据题意列出方程得（　　）

  A．234（1+x）2=345	B．234（1-2x）=345
  C．234（1+2x）=345	D．234（1-x）2=345
  组卷：790引用：8难度：0.6

  解析

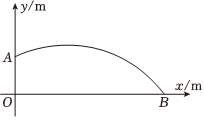• 8．小明在期末体育测试中掷出的实心球的运动路线呈抛物线形，若实心球运动的抛物线的解析式为y=-

  1

  9

  （x-3）²+k,其中y是实心球飞行的高度，x是实心球飞行的水平距离，已知该同学出手点A的坐标为（0，

  16

  9

  ），则实心球飞行的水平距离OB的长度为（　　）

  A．7m

  B．7.5m

  C．8m

  D．8.5m
  组卷：272引用：3难度：0.6

  解析

三、解答题（共9小题，满分72分）

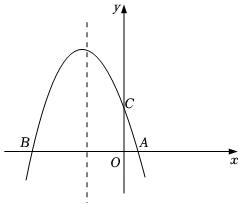• 24．如图，抛物线y=-x²+bx+c与x轴交于A（2，0），B（-6，0）两点．
  （1）求该抛物线的解析式；
  （2）若抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
  （3）在坐标平面内是否存在一点P，使得Q、B、A、P围成的图形是平行四边形，若存在，直接写出点P的坐标；若不存在，请说明理由．
  组卷：431引用：3难度：0.1

  解析

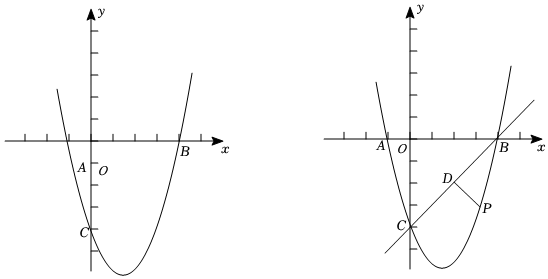
• 25．如图，在平面直角坐标系中，抛物线y=x²+bx+c与x轴交于点A（-1，0）和点B（4，0），与y轴交于点C，点P是抛物线在第四象限内图象上的一个动点，过点P作PD⊥BC于点D．
  
  （1）求抛物线的解析式；
  （2）当

  2

  PD取得最大值时，求点P的坐标和

  2

  PD的最大值；
  （3）将抛物线向右平移

  5

  2

  个单位得到新抛物线，Q为新抛物线对称轴上的一点．当（2）中

  2

  PD取得最大值时，直接写出使以点A、P、Q为顶点的三角形是直角三角形的点Q的坐标．
  组卷：506引用：3难度：0.3

  解析