2022-2023学年安徽省合肥市肥西县上派中学八年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）

• 1．在平面直角坐标系中，下列各点在第四象限的是（　　）

  A．（-1，-2）

  B．（1，-2）

  C．（1，2）

  D．（-1，2）
  组卷：214引用：6难度：0.7

  解析

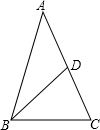• 2．如图，已知BD是△ABC的中线，AB=5，BC=3，且△ABD的周长为11，则△BCD的周长是（　　）

  A．9

  B．14

  C．16

  D．不能确定
  组卷：1527引用：8难度：0.9

  解析

• 3．在函数y=

  3

  x

  +

  2

  中，自变量x的取值范围是（　　）

  A．x≠- 2 3

  B．x＞- 2 3

  C．x≥- 2 3

  D．x≤- 2 3
  组卷：134引用：6难度：0.9

  解析

• 4．无论m为什么实数时，直线y=mx+m-2总经过点（　　）

  A．（0，-2）

  B．（-1，-2）

  C．（1，-2）

  D．（2，0）
  组卷：184引用：3难度：0.9

  解析

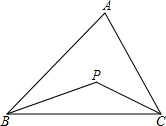• 5．如图，△ABC的两内角平分线交于点P，∠A=50°，则∠BPC=（　　）

  A．100°

  B．115°

  C．120°

  D．130°
  组卷：145引用：3难度：0.7

  解析

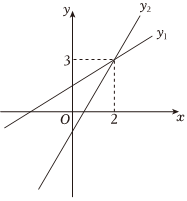• 6．一次函数y₁=a₁x+b₁与y₂=a₂x+b₂的图象在同一平面直角坐标系中的位置如图所示，小华根据图象写出下面三条信息：
  ①a₁＞0，b₁＜0；
  ②不等式a₁x+b₁≤a₂x+b₂的解集是x≥2；
  ③方程组

  y = a 1 x + b 1

  y = a 2 x + b 2

  的解是

  x = 2

  y = 3

  ．
  你认为小华写正确（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：189引用：3难度：0.5

  解析

• 7．若AD是△ABC的中线，下列结论错误的是（　　）

  A．AB=BC	B．BD=DC
  C．S△ABD=S△ACD	D．BC=2DC
  组卷：81引用：4难度：0.6

  解析

七、（本题满分12分）

• 22．阅读下面的材料，并解答问题：
  问题1：已知正数，有下列命题

  若

  a

  +

  b

  =

  2

  ，

  则

  ab

  ≤

  1

  ；

  若

  a

  +

  b

  =

  3

  ，

  则

  ab

  ≤

  3

  2

  ；

  若

  a

  +

  b

  =

  6

  ，

  则

  ab

  ≤

  3

  ；
  根据以上三个命题所提供的规律猜想：

  若

  a

  +

  b

  =

  9

  ，

  则

  ab

  ≤

   

  ，
  以上规律可表示为a+b

   

  2

  ab

  
  问题2：建造一个容积为8立方米，深2米的长方形无盖水池，池底和池壁的造价分别为每平方米120元和80元．
  （1）设池长为x米，水池总造价为y（元），求y和x的函数关系式；
  （2）应用“问题1”题中的规律，求水池的最低造价．
  组卷：161引用：10难度：0.5

  解析

八、（本题满分14分）

• 23．问题情景：如图1，在同一平面内，点B和点C分别位于一块直角三角板PMN的两条直角边PM，PN上，点A与点P在直线BC的同侧，若点P在△ABC内部，试问∠ABP，∠ACP与∠A的大小是否满足某种确定的数量关系？
  
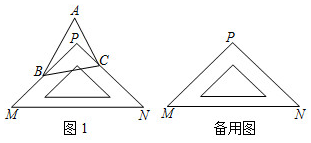
  （1）特殊探究：若∠A=55°，则∠ABC+∠ACB=

  度，∠PBC+∠PCB=

  度，∠ABP+∠ACP=

  度；
  （2）类比探索：请猜想∠ABP+∠ACP与∠A的关系，并说明理由；
  （3）类比延伸：改变点A的位置，使点P在△ABC外，其它条件都不变，判断（2）中的结论是否仍然成立？若成立，请说明理由；若不成立，请直接写出∠ABP，∠ACP与∠A满足的数量关系式．
  组卷：2628引用：14难度：0.4

  解析