当前位置：试卷中心 > 试卷详情

2022-2023学年广东省中山市八年级（下）期末数学试卷

发布：2024/6/30 8:0:9

1．要使
x
-
1
在实数范围内有意义，则x的取值范围是（　　）
A．x≤1 B．x＞1 C．x≥0 D．x≥1
组卷：485引用：12难度：0.9
解析
2．下列各式中，属于最简二次根式的是（　　）
A．
2
B．
9
C．
1
2
D．
12
组卷：60引用：2难度：0.7
解析
3．在某次“汉字听写大赛”选拔赛中，甲、乙两位同学5轮比赛成绩的平均分都是95分，其中甲的成绩方差是12，乙的成绩方差是4，则下列说法正确的是（　　）
A．甲、乙的成绩一样稳定
B．甲的成绩比乙的成绩稳定
C．乙的成绩比甲的成绩稳定
D．无法确定甲、乙的成绩谁更稳定
组卷：38引用：2难度：0.7
解析
4．下列长度的三条线段能组成直角三角形的是（　　）
A．1，1，2 B．1，2，3 C．1，1，
2
D．2，3，4
组卷：48引用：1难度：0.7
解析
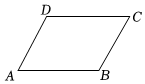5．如图，在平行四边形ABCD中，∠A+∠C=120°，则∠C的度数为（　　）
A．50° B．60° C．70° D．120°
组卷：1575引用：20难度：0.9
解析
6．下列选项中，矩形一定具有的性质是（　　）
A．对角线相等
B．对角线互相垂直
C．邻边相等
D．一条对角线平分一组对角
组卷：200引用：4难度：0.8
解析
7．如图，A，C之间隔有一湖，在与AC方向成90°角的CB方向上的点B处测得AB=500m,BC=400m,则AC的长为（　　）
A．300m B．400m C．500m D．600m
组卷：214引用：2难度：0.7
解析

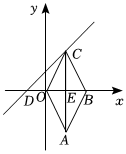22．如图，已知四边形OABC为菱形，点B在x轴上，过点C的直线CD交x轴于点D．其中直线CD的解析式为y=x+1，点B的坐标为（2，0），连接AC交x轴于点E．
（1）求AC的长；
（2）点P为x轴下方直线CD上一点，若△COP的面积为菱形OABC的面积一半，求点P的坐标．
组卷：146引用：1难度：0.6
解析
23．定义“点P对图形Q的可视度”：在平面直角坐标系中，对于点P和图形Q，若图形Q上所有的点都在∠P的内部或∠P的边上，则∠P的最小值称为点P对图形Q的可视度．如图1，点O对线段AB的可视度为∠AOB的度数．

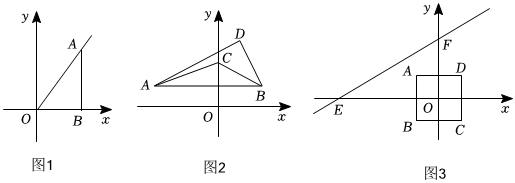
（1）如图2，已知点A（-3，1），B（2，1），C（0，2），D（1，3）．连接DA，DB，则∠ADB的度数为点D对△ABC的可视度．求证：∠ADB=90°；
（2）如图3，已知四边形ABCD为正方形，其中点A（-1，1），B（-1，-1）．直线
y
=
3
3
x
+
b
与x轴交于点E，与y轴交于点F，其中点F对正方形ABCD的可视度为60°，求点E的坐标；
（3）在（2）的条件下，在平面直角坐标系内是否存在点M，使以点A，B，E，M为顶点的四边形为平行四边形？若存在，请直接写出点M坐标；若不存在，请说明理由．
组卷：202引用：1难度：0.6
解析