2022-2023学年广东省惠州市惠东县九年级(上)核心素养数学试卷(复评)
发布:2024/7/19 8:0:9
一、选择题(本题共10小题,每题3分,共30分)
-
1.下列方程中,是一元二次方程的是( )
组卷:57引用:7难度:0.8 -
2.下列图形中,为中心对称图形的是( )
组卷:19引用:3难度:0.7 -
3.下列抛物线中,其顶点是抛物线的最高点的是( )
组卷:139引用:5难度:0.6 -
4.将y=2x2先向上平移2个单位,再向左平移3个单位,则所得解析式是( )
组卷:108引用:5难度:0.8 -
5.在平面直角坐标系中,点P(-1,-2)关于原点对称的点的坐标是( )
组卷:2012引用:21难度:0.8 -
6.对于二次函数y=(x-2)2+1的图象,下列说法正确的是( )
组卷:177引用:4难度:0.7 -
7.已知△ABC的三边长为a,b,c,且满足方程a2x2-(c2-a2-b2)x+b2=0,则方程根的情况是( )
组卷:332引用:9难度:0.6
三、解答题(三)(本题共2小题,每题12分,共24分)
-
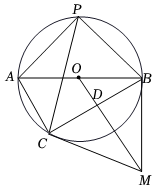 22.如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
22.如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
(1)求证:MC是⊙O的切线;
(2)若AB=20,BC=16,连接PC,求PC的长;
(3)试探究AC、BC与PC之间的数量关系,并说明理由.组卷:450引用:4难度:0.3 -
23.如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数及直线BC的表达式.
(2)过点P作PD∥y轴交直线BC于点D,求PD的最大值.
(3)点M为抛物线对称轴上的点,问在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠NMO为直角,若存在,请直接写出点N的坐标;若不存在,请说明理由.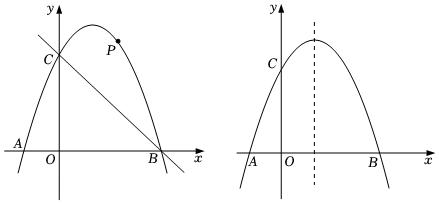 组卷:1068引用:8难度:0.3
组卷:1068引用:8难度:0.3


