2023-2024学年北京161中九年级(上)期中数学试卷
发布:2024/10/1 5:0:1
一.选择题(本题共16分,每小题2分)
-
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中既是轴对称图形,又是中心对称图形的是( )
组卷:2619引用:78难度:0.9 -
2.正方形绕着它的中心旋转,要想与原来的图形重合,至少要旋转( )
组卷:69引用:5难度:0.9 -
3.抛物线y=2(x+9)2-3的顶点坐标是( )
组卷:2987引用:55难度:0.8 -
4.一元二次方程x2-x-1=0的根的情况是( )
组卷:203引用:8难度:0.9 -
 5.如图,点A,B,C在⊙O上,连结AB,AC,OB,OC.若∠BAC=50°,则∠BOC的度数是( )组卷:1941引用:22难度:0.9
5.如图,点A,B,C在⊙O上,连结AB,AC,OB,OC.若∠BAC=50°,则∠BOC的度数是( )组卷:1941引用:22难度:0.9 -
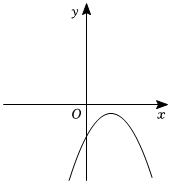 6.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )组卷:1633引用:13难度:0.8
6.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )组卷:1633引用:13难度:0.8 -
7.已知点A(-1,y1),B(-2,y2),C(-4,y3)在抛物线y=2x2+8x-1上,则y1,y2,y3的大小关系是( )
组卷:887引用:12难度:0.8 -
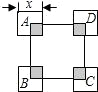 8.如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是( )组卷:614引用:54难度:0.7
8.如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是( )组卷:614引用:54难度:0.7
二、填空题(本题共16分,每小题2分)
-
9.方程x2=6x的解为 .
组卷:845引用:22难度:0.9
三、解答题(本题共68分,其中17-21每题5分,22题6分,23题5分,24题-26题每题6分,27-28每题7分)
-
27.在Rt△ABC中,∠ACB=90°,AC=1,记∠ABC=α,点D为射线BC上的动点,连接AD,将射线DA绕点D顺时针旋转α角后得到射线DE,过点A作AD的垂线,与射线DE交于点P,点B关于点D的对称点为Q,连接PQ.
(1)当△ABD为等边三角形时,
①依题意补全图1;
②PQ的长为 ;
(2)如图2,当α=45°,且时,求证:PD=PQ.BD=43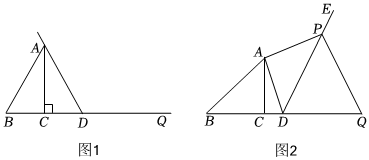 组卷:79引用:2难度:0.4
组卷:79引用:2难度:0.4 -
28.如图1,对于△PMN的顶点P及其对边MN上的一点Q,给出如下定义:以P为圆心,PQ为半径的圆与直线MN的公共点都在线段MN上,则称点Q为△PMN关于点P的内联点.
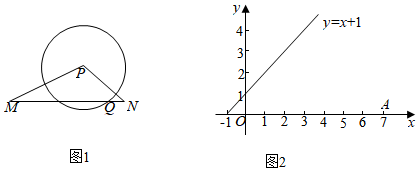
在平面直角坐标系xOy中:
(1)如图2,已知点A(7,0),点B在直线y=x+1上.
①若点B(3,4),点C(3,0),则在点O,C,A中,点 是△AOB关于点B的内联点;
②若△AOB关于点B的内联点存在,求点B纵坐标n的取值范围;
(2)已知点D(2,0),点E(4,2),将点D绕原点O旋转得到点F.若△EOF关于点E的内联点存在,直接写出点F横坐标m的取值范围.组卷:1090引用:9难度:0.1


