2022-2023学年广东省东莞市东华初级中学八年级（下）期中数学试卷

一、选择题（共10题，每小题3分，共30分）

• 1．要使二次根式

  x

  +

  1

  有意义，则x的取值范围是（　　）

  A．x≥-1	B．x＜-1
  C．x≠0	D．x为任意实数
  组卷：319引用：7难度：0.9

  解析

• 2．下列计算正确的是（　　）

  A． 4 + 5 = 9

  B． （ - 2 ） 7 = - 2

  C． 18 + 3 = 6

  D． 3 2 - 2 = 2 2
  组卷：78引用：1难度：0.7

  解析

• 3．下列二次根式，最简二次根式是（　　）

  A． 8

  B． 1 2

  C． 5

  D． 27
  组卷：1916引用：24难度：0.9

  解析

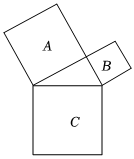• 4．如图是一株美丽的勾股树，其中所有四边形都是正方形，三角形是直角三角形，若正方形A、B的面积分别为5、3，则最大正方形C的面积是（　　）

  A．15

  B．8

  C．11

  D．13
  组卷：181引用：2难度：0.8

  解析

• 5．如图，D，E分别是△ABC的边AB，AC上的中点，若DE=12，则BC是（　　）

  A．6

  B．12

  C．18

  D．24
  组卷：113引用：4难度：0.7

  解析

• 6．菱形，矩形，正方形都具有的性质是（　　）

  A．四条边相等，四个角相等

  B．对角线相等

  C．对角线互相垂直

  D．对角线互相平分
  组卷：6264引用：59难度：0.9

  解析

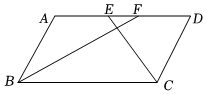• 7．如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD交AD于点E，AB=5，BC=9，则EF长为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：171引用：6难度：0.6

  解析

五、解答题（三）：（本大题共2小题，每小题12分，共24分）.

• 22．如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．
  （1）求证：△BDF是等腰三角形；
  （2）如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．
  ①判断四边形BFDG的形状，并说明理由；
  ②若AB=6，AD=8，求FG的长．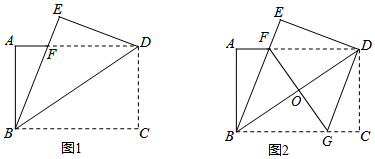
  
  组卷：2632引用：11难度：0.3

  解析

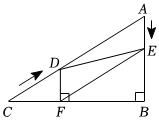• 23．如图，在Rt△ABC中，∠B=90°AC=40cm∠A=60°，点D从点C出发沿CA方向以2cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以1cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t s（0＜t≤20）．过点D作DF⊥BC于点F，连接DE，EF；
  （1）求证：四边形AEFD为平行四边形；
  （2）四边形AEFD能成为菱形吗？若能，求出相应的t值，若不能，请说明理由；
  （3）当t为何值时，△DEF为直角三角形？请说明理由．
  组卷：151引用：1难度：0.3

  解析