2023-2024学年福建省福州十一中九年级（上）月考数学试卷（10月份）

一、单选题（每题4分，共10题）

• 1．在平面直角坐标系中，点P（4，-2）关于原点对称的点的坐标是（　　）

  A．（-4，2）

  B．（4，2）

  C．（-2，4）

  D．（-4，-2）
  组卷：502引用：13难度：0.7

  解析

• 2．关于x的方程（k-1）²x²+（2k+1）x+1=0有实数根，则k的取值范围是（　　）

  A．k ＞ 1 4 且k≠1

  B．k≥ 1 4 且k≠1

  C．k ＞ 1 4

  D．k≥ 1 4
  组卷：4135引用：33难度：0.7

  解析

• 3．某商品原价400元，经连续两次降价后售价为256元，设平均每降价的百分率为x,则下面所列的方程正确的是（　　）

  A．256（1-x）2=400	B．400（1-x）2=256
  C．256（1-2x）2=400	D．400（1-2x）2=256
  组卷：88引用：4难度：0.5

  解析

• 4．关于二次函数y=-2x²+1的图象，下列说法中，正确的是（　　）

  A．对称轴为直线x=1

  B．顶点坐标为（-2，1）

  C．可以由二次函数y=-2x2的图象向左平移1个单位得到

  D．在y轴的左侧，图象上升，在y轴的右侧，图象下降
  组卷：739引用：10难度：0.7

  解析

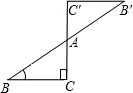• 5．如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=30°，BC=1，则BB′的长为（　　）

  A．4

  B． 3 3

  C． 2 3 3

  D． 4 3 3
  组卷：568引用：41难度：0.7

  解析

• 6．2022年的卡塔尔世界杯受到广泛关注，在半决赛中，梅西的一脚射门将足球沿着抛物线飞向球门，此时，足球距离地面的高度h与足球被踢出后经过的时间t之间的关系式为h=-t²+bt.已知足球被踢出9s时落地，那么足球到达距离地面最大高度时的时间l为（　　）

  A．3s

  B．3.5s

  C．4s

  D．4.5s
  组卷：433引用：7难度：0.7

  解析

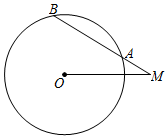• 7．⊙O的半径为5，M是圆外一点，MO=6，∠OMA=30°，则弦AB的长为（　　）

  A．4

  B．6

  C．6 3

  D．8
  组卷：3447引用：15难度：0.5

  解析

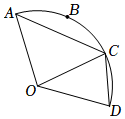• 8．如图，O是弧AD所在圆的圆心．已知点B、C将弧AD三等分，那么下列四个选项中不正确的是（　　）

  A．AC=2CD	B．∠AOC=2∠COD
  C．S扇形AOC=2S扇形COD	D． ˆ AC =2 ˆ CD
  组卷：227引用：3难度：0.5

  解析

三、解答题

• 24．如图，正方形OEFG绕着边长为a的正方形ABCD的对角线的交点O旋转，边OE、OG分别交边AD、AB于点M、N．
  （1）求证：OM=ON；
  （2）问四边形OMAN的面积是否随着a的变化而变化？若不变，请用a的代数式表示出来，若变化，请说明理由；
  （3）试探究PA、PN、BN三条线段之间有怎样的数量关系，并写出推理过程．
  组卷：54引用：4难度：0.5

  解析

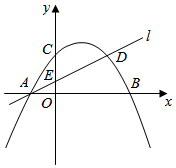• 25．如图，抛物线y=ax²+bx+c与x轴交于A（-2，0）、B（6，0）两点，与y轴交于点C．直线l与抛物线交于A、D两点，与y轴交于点E，点D的坐标为（4，3）．
  （1）求抛物线的解析式与直线l的解析式；
  （2）若点P是抛物线上的点且在直线l上方，连接PA、PD，求当△PAD面积最大时点P的坐标及该面积的最大值；
  （3）若点Q是y轴上的点，且∠ADQ=45°，求点Q的坐标．
  组卷：5351引用：11难度：0.1

  解析