2020-2021学年河南省南阳市西峡县八年级（上）期末数学试卷

一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的。

• 1．小明同学在做掷骰子游戏实验中，投掷了100次正方体骰子，不同点数出现的情况如下表所示：
  

  出现点数	1	2	3	4	5	6
  次数	20	15	13	19	16	17

  则出现点数5的频数与频率分别是（　　）

  A．15和0.15

  B．16和0.16

  C．16和0.32

  D．16和100
  组卷：7引用：1难度：0.8

  解析

• 2．

  （

  -

  9

  ）

  2

  的平方根是（　　）

  A．-9

  B．±9

  C．3

  D．±3
  组卷：149引用：2难度：0.7

  解析

• 3．运算（-a²b）³÷（ab）²的结果是（　　）

  A．a4b

  B．a2b

  C．-a4b

  D．-a2b
  组卷：127引用：3难度：0.8

  解析

• 4．将多项式（x²-

  1

  2

  x

  +

  1

  16

  ）-y²分解因式的结果是（　　）

  A．（x- 1 4 ）2-y2	B．（x + y - 1 4 ）（x + y + 1 4 ）
  C．（x + y - 1 4 ）（x-y- 1 4 ）	D．（x-y- 1 4 ）（x-y+ 1 4 ）
  组卷：91引用：1难度：0.8

  解析

• 5．已知2a+b=c+3，则（4^a•2^b）÷2^c的值等于（　　）

  A．8

  B．4

  C．16

  D．32
  组卷：11引用：1难度：0.7

  解析

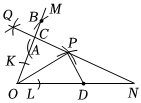• 6．已知∠MON，按下列方法作图：
  ①以点O为圆心，以适当长度为半径作弧分别交OM、ON于K、L；
  ②分别以K、L为圆心，以大于

  1

  2

  KL

  长度为半径作弧相交于点P；
  ③作射线OP；
  ④以点P为圆心，以适当的长度为半径作弧交OM于点A、B；
  ⑤分别以A、B为圆心，以适当长度为半径作弧相交于点Q；
  ⑥作直线PQ，交OM于C．
  若OP=10，OC=8，PN=14，点D是线段ON上的动点，设PD=x,则x的取值范围（　　）

  A．6≤x≤10

  B．10≤x≤14

  C．6≤x≤14

  D．8≤x≤14
  组卷：19引用：1难度：0.7

  解析

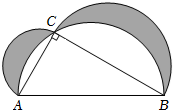• 7．如图，在△ABC中，∠C=90°，AC=6，BC=8，分别以AC、BC、AB为直径向AB的同侧作半圆，三个半圆和三角形的边围成了阴影部分的图形．则图中阴影部分的面积是（　　）

  A． 25 π 2 - 24

  B． 25 π 2

  C．24

  D．25
  组卷：30引用：1难度：0.5

  解析

三、解答题（8个小题，共75分）

• 22．阅读材料：
  我们曾经解决过如下问题：“如图1，点M，N分别在直线AB同侧，如何在直线AB上找到一个点P，使得PM+PN最小？”
  我们可以经过如下步骤解决这个问题：
  （1）画草图（或目标图）分析思路：在直线AB上任取一点P′，连接P′M，P′N，根据题目需要，作点M关于直线AB的对称点M′，将P′M+P′N转化为P′M′+P′N′，“化曲为直”寻找P′M′+P′N的最小值；
  （2）设计画图步骤；
  （3）回答结论并验证．
  解决下列两个问题：
  （1）如图2，在△ABC中，AB=3，AC=4，BC=5，EF垂直且平分BC，点P在直线EF上，直接写出PA+PB的最小值，回答PA+PB取最小值时点P的位置并在图中标出来；解：PA+PB的最小值为

   

  ，PA+PB取最小值时点P的位置是

   

  ；
  （2）如图3，点M，N分别在直线AB两侧，在直线AB上找一点P，使得∠MPB=∠NPB．要求画图，并简要叙述确定点P位置的步骤．（无需尺规作图，保留画图痕迹，无需证明）
  解：确定点P位置的简要步骤：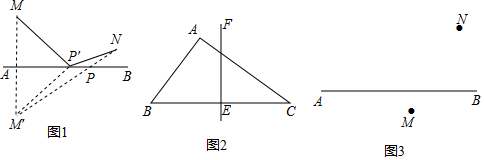

   

  ．
  
  组卷：256引用：3难度：0.5

  解析

• 23．（1）观察发现：我们知道：“等腰三角形顶角平分线、底边上的高和中线三线合一”．猜想：如图1，在△ABC中，如果∠1=∠2，AD⊥BC于D，那么△ABC是等腰三角形吗？如果是，请证明；如果不是，请说明理由．
  （2）拓展应用：如图2，已知在△ABC中，AD平分角∠BAC，AD⊥BD，∠ABC=3∠C．求证：AB+2BD=AC．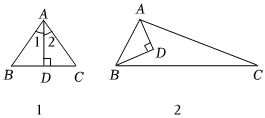
  
  组卷：83引用：1难度：0.5

  解析