2023-2024学年山东省德州市禹城市高新区九年级(上)第一次月考数学试卷
发布:2024/9/9 4:0:8
一、选择题(本大题共12小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
-
1.关于x的一元二次方程x2-(k-1)x-k+2=0有两个实数根x1,x2,若(x1-x2+2)(x1-x2-2)+2x1x2=-3,则k的值( )
组卷:6013引用:20难度:0.5 -
2.宾馆有50间房供游客居住,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )
组卷:5177引用:42难度:0.7 -
3.商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)
以及实数x(0<x<1)确定实际销售价格c=a+x(b-a),这里x被称为乐观系数.经验表明,最佳乐观系数x恰好使得,据此可得,最佳乐观系数x的值等于( )b-ac-a=c-ab-c组卷:1405引用:8难度:0.3 -
4.将二次函数y=x2-5x-6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
组卷:6874引用:21难度:0.4 -
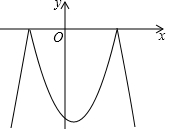 5.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),当直线y=-x+m与新图象有4个交点时,m的取值范围是( )组卷:6417引用:25难度:0.7
5.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),当直线y=-x+m与新图象有4个交点时,m的取值范围是( )组卷:6417引用:25难度:0.7 -
6.在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个完美点(
,32),且当0≤x≤m时,函数y=ax2+4x+c-32(a≠0)的最小值为-3,最大值为1,则m的取值范围是( )34组卷:4544引用:30难度:0.3 -
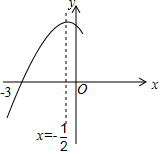 7.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0),其对称轴为直线x=-,结合图象分析下列结论:12
7.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0),其对称轴为直线x=-,结合图象分析下列结论:12
①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④一元二次方程cx2+bx+a=0的两根分别为x1=-,x2=13;12
⑤<0;b2-4ac4a
⑥若m,n(m<n)为方程a(x+3)(x-2)+3=0的两个根,则m<-3且n>2,
其中正确的结论有( )组卷:3321引用:15难度:0.6 -
8.已知关于x的方程(k-2)2x2+(2k+1)x+1=0有实数根,则k的取值范围是( )
组卷:504引用:7难度:0.8
三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
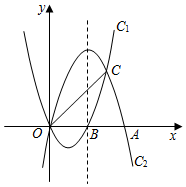 25.如图,抛物线C1:y=x2-2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
25.如图,抛物线C1:y=x2-2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.组卷:5069引用:12难度:0.4 -
26.已知:抛物线C1:y=-(x+m)2+m2(m>0),抛物线C2:y=(x-n)2+n2(n>0),称抛物线C1,C2互为派对抛物线,例如抛物线C1:y=-(x+1)2+1与抛物线C2:y=(x-
)2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.2
(1)已知抛物线①y=-x2-2x,②y=(x-3)2+3,③y=(x-)2+2,④y=x2-x+2,则抛物线①②③④中互为派对抛物线的是(请在横线上填写抛物线的数字序号);12
(2)如图1,当m=1,n=2时,证明AC=BD;
(3)如图2,连接AB,CD交于点F,延长BA交x轴的负半轴于点E,记BD交x轴于G,CD交x轴于点H,∠BEO=∠BDC.
①求证:四边形ACBD是菱形;
②若已知抛物线C2:y=(x-2)2+4,请求出m的值.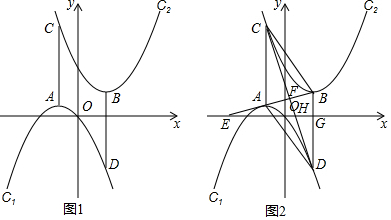 组卷:767引用:6难度:0.3
组卷:767引用:6难度:0.3


