2022-2023学年广东省惠州市博罗县平安中学八年级（上）开学数学试卷

一、单选题：本大题共9小题，每小题3分，共30分。

• 1．点P（m+3，m-1）在x轴上，则点P的坐标为（　　）

  A．（0，-2）

  B．（2，0）

  C．（4，0）

  D．（0，-4）
  组卷：9131引用：43难度：0.9

  解析

• 2．正比例函数y=kx（k≠0）的函数值y随x的增大而增大，则一次函数y=x+k的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：2236引用：50难度：0.9

  解析

• 3．某工艺品厂草编车间共有16名工人，为了了解每个工人的日均生产能力，随机调查了某一天每个工人的生产件数．获得数据如下表：
  

  生产件数（件）	10	11	12	13	14	15
  人数（人）	1	5	4	3	2	1

  则这一天16名工人生产件数的众数是（　　）

  A．5件

  B．11件

  C．12件

  D．15件
  组卷：432引用：5难度：0.9

  解析

• 4．某篮球队10名队员的年龄结构如表，已知该队队员年龄的中位数为21.5，则众数与方差分别为（　　）
  

  年龄	19	20	21	22	24	26
  人数	1	1	x	y	2	1

  A．22，3

  B．22，4

  C．21，3

  D．21，4
  组卷：674引用：13难度：0.7

  解析

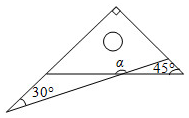• 5．将一副直角三角板如图放置，使两直角边重合，则∠α的度数为（　　）

  A．75°

  B．105°

  C．135°

  D．165°
  组卷：3873引用：30难度：0.8

  解析

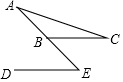• 6．如图，BC∥DE，若∠A=35°，∠C=24°，则∠E等于（　　）

  A．24°

  B．59°

  C．60°

  D．69°
  组卷：936引用：16难度：0.7

  解析

• 7．如图，直线y=-

  4

  3

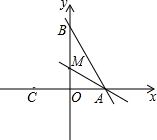  x+8与x轴、y轴分别交于A、B两点，点M是OB上一点，若直线AB沿AM折叠，点B恰好落在x轴上的点C处，则点M的坐标是（　　）

  A．（0，4）

  B．（0，3）

  C．（-4，0）

  D．（0，-3）
  组卷：2293引用：8难度：0.7

  解析

• 8．如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=

  5

  ，则BC的长为（　　）

  A． 3 -1

  B． 3 +1

  C． 5 -1

  D． 5 +1
  组卷：4598引用：69难度：0.7

  解析

三、解答题：第18，19，20小题6分，第21，22，23小题8分，第24，25小题10分。

• 23．已知：如图1，∠1+∠2=180°，∠AEF=∠HLN；
  （1）判断图中平行的直线，并给予证明；
  （2）如图2，∠PMQ=2∠QMB，∠PNQ=2∠QND，请判断∠P与∠Q的数量关系，并证明．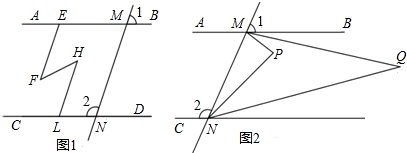
  
  组卷：2014引用：6难度：0.5

  解析

• 24．如图①，在△ABC中，CD⊥AB于点D，AD=CD=2，BD=4，点E是线段BD的中点，点P从点A出发，沿折线AC-CB向终点B运动，点P在边AC上的速度为每秒

  2

  个单位长度，点P在边BC上的速度为

  5

  个单位长度，设点P的运动时间为t（秒）．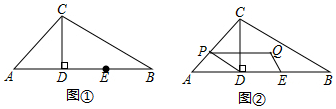
  
  （1）用含t的代数式表示点P到直线AB的距离．
  （2）如图②，作点P关于直线CD的对称点Q，设以D、E、Q、P为顶点的四边形的面积为S（平方单位），求S与t之间的函数关系式．
  （3）当点P在边BC上时，在△BCD的边上（不包括顶点）存在点H，使四边形DEPH为轴对称图形，直接写出此时线段CP的长．
  组卷：381引用：10难度：0.1

  解析