人教新版八年级上册《13.3 等腰三角形》2023年同步练习卷（5）
发布：2024/9/13 6:0:10
一、选择题
-
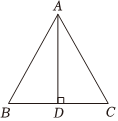1．如图，△ABC中，AB=AC，AD⊥BC，下列结论不正确的是（ ）组卷：587引用：8难度：0.7 -
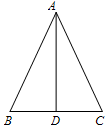2．如图，在△ABC中，AB=AC，AD是△ABC的中线．若∠CAD=25°，则∠B的度数是（ ）组卷：572引用：7难度：0.7 -
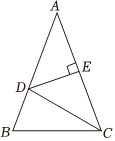3．如图，在△ABC中，AB=AC，∠A=40°，DE垂直平分AC，则∠BCD的度数等于（ ）组卷：497引用：9难度：0.7 -
4．若等腰△ABC中有一个内角为40°，则这个等腰三角形的一个底角的度数为（ ）
组卷：1092引用：5难度：0.6 -
5．下列能断定△ABC为等腰三角形的是（ ）
组卷：1162引用：11难度：0.7 -
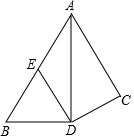6．如图，AD平分∠BAC，AD⊥BD于D，DE∥AC，则图中的等腰三角形的个数为（ ）组卷：285引用：3难度：0.6 -
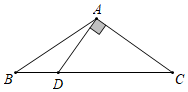7．如图，△ABC中，AB=AC，过点A作DA⊥AC交BC于点D．若∠B=2∠BAD，则∠BAD的度数为（ ）组卷：1186引用：11难度：0.7 -
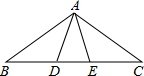8．如图所示，在三角形ABC中，AB=AC，∠BAC=108°，在BC上分别取点D，E使∠BAD=∠B，∠CAE=∠C，则图中的等腰三角形有（ ）组卷：349引用：5难度：0.5 -
9．等腰三角形的一个角比另一个角2倍少20度，等腰三角形顶角的度数是（ ）
组卷：3998引用：12难度：0.5
三、解答题
-
28．数学课上，张老师举了下面的例题：
例1：等腰△ABC中，∠A=100°，求∠B的度数（答案：40°）
例2：等腰△ABC中，∠A=50°，求∠B的度数（答案：50°或65°或80°）
张老师启发同学们进行变式，小敏编了如下一题：
变式：等腰△ABC中，∠A=70°，求∠B的度数
（1）请你解答小敏编的变式题；
（2）解第（1）小题后小敏发现，∠A的度数不同得到∠B的度数的个数也可能不同．如果在等腰△ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．组卷：320引用：2难度：0.6 -
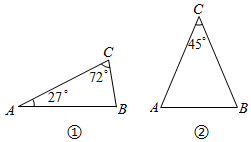29．【定义】如果1条线段将一个三角形分成2个等腰三角形，那么这1条线段就称为这个三角形的“好线”，如果2条线段将一个三角形分成3个等腰三角形，那么这2条线段就称为这个三角形的“好好线”．
【理解】如图①，在△ABC中，∠A=27°，∠C=72°，请你在这个三角形中画出它的“好线”，并标出等腰三角形顶角的度数．
如图②，已知△ABC是一个顶角为45°的等腰三角形，请你在这个三角形中画出它的“好好线”，并标出所分得的等腰三角形底角的度数．
【应用】
（1）在△ABC中，已知一个内角为24°，若它只有“好线”，请你写出这个三角形最大内角的所有可能值；（按从小到大写）
（2）在△ABC中，∠C=27°，AD和DE分别是△ABC的“好好线”，点D在BC边上，点E在AB边上，且AD=DC，BE=DE，根据题意写出∠B的度数的所有可能值．组卷：246引用：2难度：0.2
