2021-2022学年福建省三明市明溪县八年级（上）期中数学试卷

一、选择题（每小题4分，共40分）

• 1．已知△ABC的一个外角为50°，则△ABC一定是（　　）

  A．锐角三角形

  B．钝角三角形

  C．直角三角形

  D．锐角三角形或钝角三角形
  组卷：1461引用：23难度：0.9

  解析

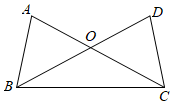• 2．如图，下列条件中，能证明△ABC≌△DCB的是（　　）

  A．AB=DC，AC=DB	B．AB=DC，∠ABC=∠DCB
  C．BO=CO，∠A=∠D	D．AB=DC，∠A=∠D
  组卷：50引用：3难度：0.5

  解析

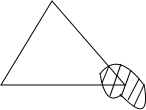• 3．如图所示，小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他根据的定理是（　　）

  A．SSS

  B．SAS

  C．AAS

  D．ASA
  组卷：645引用：9难度：0.9

  解析

• 4．如图，将Rt△ABC（其中∠B=34°，∠C=90°）绕A点按顺时针方向旋转到△AB₁C₁的位置，使得点C，A，B₁在同一条直线上，那么旋转角最小等于（　　）

  A．56°

  B．68°

  C．124°

  D．180°
  组卷：283引用：30难度：0.7

  解析

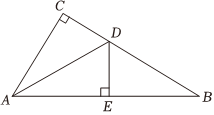• 5．如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE=1，则BC=（　　）

  A． 3

  B．2

  C．3

  D． 3 +2
  组卷：6698引用：85难度：0.9

  解析

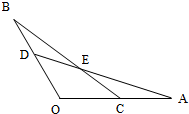• 6．如图，OA=OB，∠A=∠B，有下列3个结论：
  ①△AOD≌△BOC，
  ②△ACE≌△BDE，
  ③点E在∠O的平分线上，
  其中正确的结论是（　　）

  A．只有①

  B．只有②

  C．只有①②

  D．有①②③
  组卷：1050引用：19难度：0.9

  解析

• 7．平面直角坐标系中的点P（2-m,

  1

  2

  m）关于x轴的对称点在第四象限，则m的取值范围在数轴上可表示为（　　）

  A．	B．
  C．	D．
  组卷：757引用：52难度：0.9

  解析

• 8．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（　　）

  A．60°

  B．72°

  C．90°

  D．108°
  组卷：3370引用：139难度：0.9

  解析

三、解答题（共78分）

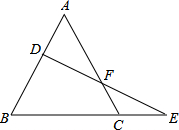• 25．已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．
  求证：AD=CE．
  组卷：3368引用：61难度：0.5

  解析

• 26．（1）问题发现
  如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
  填空：①∠AEB的度数为

  ；
  ②线段AD，BE之间的数量关系为

  ．
  （2）拓展探究
  如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．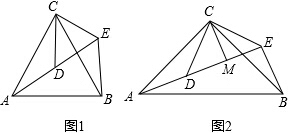
  
  组卷：5047引用：35难度：0.5

  解析