2023-2024学年广东省深圳市南山外国语学校（集团）九年级（上）期中数学试卷

一、选择题（每题3分，共30分）

• 1．下列是一元二次方程的是（　　）

  A．ax2+bx+c=0

  B．2x2-y+1=0

  C． x 2 - 1 x 2 = 0

  D．x2+2x=0
  组卷：225引用：3难度：0.8

  解析

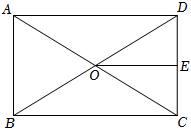• 2．如图，矩形ABCD的对角线AC、BD相交于点O，点E是CD的中点，若OE=3，则BC的长为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：2146引用：14难度：0.8

  解析

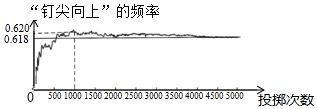• 3．如图显示了用计算机模拟随机投掷一枚图钉的实验结果．随着试验次数的增加，“钉尖向上”的频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是（　　）

  A．0.620

  B．0.618

  C．0.610

  D．1000
  组卷：1024引用：17难度：0.9

  解析

• 4．平行四边形、矩形、菱形、正方形都具有的性质是（　　）

  A．对边平行且相等

  B．对角线互相垂直

  C．每条对角线平分一组对角

  D．四边相等
  组卷：1079引用：13难度：0.9

  解析

• 5．下列平行四边形中，根据图中所标出的数据，不一定是菱形的是（　　）

  A．

  B．

  C．

  D．
  组卷：2000引用：22难度：0.8

  解析

• 6．若关于x的方程（m-1）x²+4x+1=0有实数根，则m的取值范围是（　　）

  A．m≤5且m≠1

  B．m≥5

  C．m≤5

  D．m＜5
  组卷：500引用：2难度：0.5

  解析

• 7．有一个人患了流行性感冒，经过两轮传染后共有196人患病，则每轮传染中平均一个人传染的人数是（　　）人．

  A．13

  B．14

  C．15

  D．16
  组卷：957引用：7难度：0.5

  解析

三．解答题（共55分）

• 21．综合与实践．
  （1）提出问题．如图1，在△ABC和△ADE中，∠BAC=∠DAE=90°，且AB=AC，AD=AE，连接BD，连接CE交BD的延长线于点O．
  ①∠BOC的度数是

  ．
  ②BD：CE=

  ．
  （2）类比探究．如图2，在△ABC和△DEC中，∠BAC=∠EDC=90°，且AB=AC，DE=DC，连接AD、BE并延长交于点O．
  ①∠AOB的度数是

  ；
  ②AD：BE=

  ．
  （3）问题解决．如图3，在等边△ABC中，AD⊥BC于点D，点E在线段AD上（不与A重合），以AE为边在AD的左侧构造等边△AEF，将△AEF绕着点A在平面内顺时针旋转任意角度．如图4，M为EF的中点，N为BE的中点．
  ①说明△MND为等腰三角形．
  ②求∠MND的度数．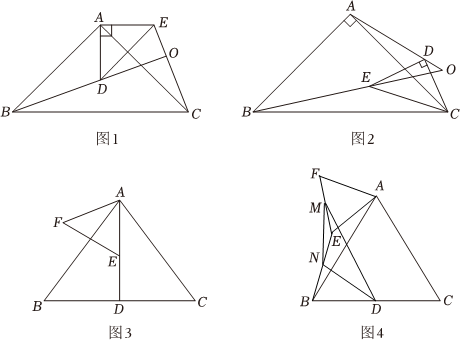
  
  组卷：2445引用：7难度：0.6

  解析

• 22．如图，在平面直角坐标系xOy中，已知点A（a,0）（a＞0），B（2，3），C（0，3）．过原点O作直线l,使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
  （Ⅰ）若点D与点A重合，则θ=

  （度），a的值为

  ；
  （Ⅱ）若θ=45°，点B落在点E处，若点E在四边形OABC的边AB上，求点A的坐标；
  （Ⅲ）作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出a的值．
  组卷：380引用：4难度：0.5

  解析