2023-2024学年山东省济南市槐荫区九年级（上）期中数学试卷
发布：2024/10/3 19:0:1
一、选择题（本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）
-
1．2cos45°的值等于（ ）
组卷：940引用：5难度：0.8 -
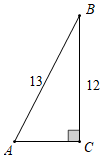2．如图，在Rt△ABC中，∠C=90°，AB=13，BC=12，下列三角函数正确的是（ ）组卷：1809引用：9难度：0.5 -
3．如图，AD∥BE∥CF，若AB=2，BC=4，EF=5，则DE的长度是（ ）组卷：741引用：9难度：0.8 -
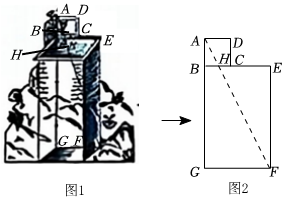4．四分仪是一种十分古老的测量仪器．其出现可追溯到数学家托勒密的《天文学大成》．图1是古代测量员用四分仪测量一方井的深度，将四分仪置于方井上的边沿，通过窥衡杆测望井底点F、窥衡杆与四分仪的一边BC交于点H．图2中，四分仪为正方形ABCD．方井为矩形BEFG．若测量员从四分仪中读得AB为1，BH为0.5，实地测得BE为2.5．则井深BG为（ ）组卷：1270引用：13难度：0.6 -
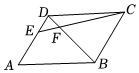5．如图，在▱ABCD中，点E在AD上，且AE=2ED，CE交对角线BD于点F，若S△DEF=2，则S△BCF为（ ）组卷：1628引用：12难度：0.7 -
6．滑雪爱好者小张从山坡滑下，为了得出滑行距离s（单位：m）与滑行时间t（单位：s）之间的关系式，测得的一些如下数据（如表），为观察：s与t之间的关系，建立坐标系（如图），以t为横坐标，s为纵坐标绘制了如图所示的函数图象
滑行时间t/s 0 1 2 3 4 滑行距离s/m 0 4.5 14 28.5 48 
根据以上信息，可知，s与t的函数关系式是（不考虑取值范围）（ ）组卷：579引用：4难度：0.7 -
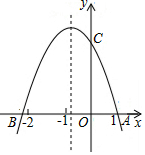7．如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B，与y轴的正半轴交于点C．现有下列结论：①abc＞0；②4a-2b+c＞0；③2a-b＞0；④3a+c=0，其中，正确结论的个数是（ ）组卷：497引用：2难度：0.5 -
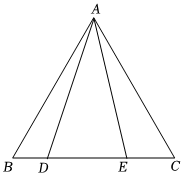8．如图，△ABC是边长为6的等边三角形，点D，E在边BC上，若∠DAE=30°，，则BD的长度是（ ）tan∠EAC=13组卷：952引用：6难度：0.6
三、解答题（本大题共10个小题，共86分.解答应写出文字说明，证明过程或演算步骤.）
-
25．【问题背景】：△ABC中，AB=AC，∠BAC=90°，P为BC上的动点，小熙拿含45°角的透明三角板，使45°角的顶点落在点P，三角板可绕P点旋转．
【用数学的眼光观察】：（1）如图1，当三角板的两边分别交AB、AC于点E、F时．以下结论正确的是：
；
①△BPE≌△CFP；
②△BPE∽△CFP；
③∠BEP=∠CPF；
④；BECP=PEFP
【用数学的思维思考】：（2）将三角板绕点P旋转到图2情形时，三角板的两边分别交BA的延长线、边AC于点E、F．△BPE与△CFP相似吗？请说明理由；
【用数学的语言表达】：
（3）在（2）的条件下，动点P运动到什么位置时，△BPE∽△PFE？说明理由．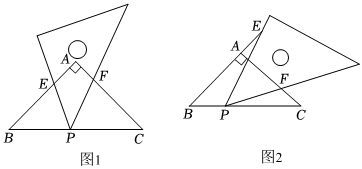
组卷：310引用：2难度：0.3 -
26．如图1，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水．喷水口H离地竖直高度为h（单位：m）．如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形DEFG，其水平宽度DE=3m,竖直高度为EF的长．下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d（单位：m）．
（1）若h=1.5，EF=0.5m.
①求上边缘抛物线的函数解析式，并求喷出水的最大射程OC；
②求下边缘抛物线与x轴的正半轴交点B的坐标；
（2）若EF=1m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带，请直接写出h的最小值．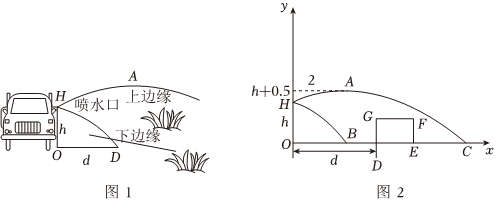
组卷：88引用：1难度：0.5
