2022-2023学年山西省吕梁市交口县八年级（上）期末数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分）

• 1．用数学的眼光观察下面的网络图标，其中可以抽象成轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：335引用：22难度：0.8

  解析

• 2．一个三角形的两条边分别为3cm,7cm,则它的第三边可能是（　　）

  A．3cm

  B．7cm

  C．10cm

  D．12cm
  组卷：290引用：9难度：0.7

  解析

• 3．新型冠状病毒呈圆形或者椭圆形，最大直径约0.00000014米，该数据用科学记数法可表示为（　　）

  A．14×10-6

  B．14×10-7

  C．1.4×10-6

  D．1.4×10-7
  组卷：498引用：4难度：0.9

  解析

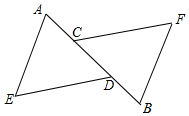• 4．如图示，点C，D在线段AB上，AC=DB，AE∥BF，添加以下哪一个条件仍然不能判定△AED≌△BFC（　　）

  A．AE=BF

  B．ED=CF

  C．∠E=∠F

  D．ED∥CF
  组卷：310引用：2难度：0.7

  解析

• 5．下列运算正确的是（　　）

  A．m+3m=3m2	B．3m2•2m3=6m6
  C．（3m）2=9m2	D．m6÷m6=m
  组卷：428引用：7难度：0.7

  解析

• 6．已知点A（m,2021）与点B（2022，n）关于y轴对称，则m+n的值为（　　）

  A．-1

  B．1

  C．4043

  D．-2022
  组卷：508引用：5难度：0.8

  解析

• 7．2022年北京冬奥会开幕式为世界奉献了一场精彩、简约、唯美、浪漫的中国文化盛宴，其中主火炬台的雪花状创意令人惊叹．如图是一个正六边形雪花状饰品，则它的每一个内角是（　　）

  A．60°

  B．105°

  C．120°

  D．135°
  组卷：718引用：17难度：0.8

  解析

三、解答题（本大题共8个小题，共70分）解答应写出文字说明，证明过程或演算步骤．

• 22．如图1，在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE=DA．
  
  （1）求证：∠BAD=∠EDC；
  （2）如图2，点M是点E关于直线BC的对称点，连接DM，AM，CM．猜想DM与AM之间的数量关系，并说明理由．
  组卷：149引用：1难度：0.5

  解析

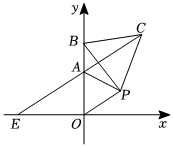• 23．如图，在平面直角坐标系中，△AOP为等边三角形，A点坐标为（0，1），点B在y轴上且位于A点上方，以BP为边向BP的右侧作等边△PBC，连接CA，并延长CA交x轴于点E．
  （1）求证：OB=AC；
  （2）判断AP是否平分∠OAC？请说明理由；
  （3）在y轴上是否存在点Q，使得△AEQ为等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
  组卷：208引用：4难度：0.3

  解析