2022-2023学年湖北省黄石市黄石港区八年级（下）期末数学试卷

一、选择题（每题3分，共30分

• 1．下列式子是最简二次根式的是（　　）

  A． 4

  B． 12

  C． 13

  D． 0 . 3
  组卷：1046引用：14难度：0.7

  解析

• 2．在△ABC中，∠A，∠B，∠C的对边分别记为a,b,c,下列条件中，能判定△ABC是直角三角形的是（　　）

  A．a=1，b=2，c=3	B．a2=（c-b）（c+b）
  C．∠A=∠C	D．∠A：∠B：∠C=3：4：5
  组卷：257引用：2难度：0.7

  解析

• 3．下列计算正确的是（　　）

  A．3+ 2 =3 2

  B．（ 3 5 ）2=15

  C． 9 2 = 3 2

  D． 8 - 2 = 2
  组卷：94引用：3难度：0.7

  解析

• 4．如图，在平行四边形ABCD中，已知∠ODA=90°，AC=10cm,BD=6cm,则AD的长为（　　）

  A．4cm

  B．5cm

  C．6cm

  D．8cm
  组卷：979引用：39难度：0.9

  解析

• 5．若直线y=2x+1与y=-x+b的交点在第一象限，则b的值可以是（　　）

  A．2

  B．1

  C．0

  D．-1
  组卷：248引用：4难度：0.6

  解析

• 6．在庆祝新中国成立70周年的校园歌唱比赛中，11名参赛同学的成绩各不相同，按照成绩取前5名进入决赛．如果小明知道了自己的比赛成绩，要判断能否进入决赛，小明需要知道这11名同学成绩的（　　）

  A．平均数

  B．中位数

  C．众数

  D．方差
  组卷：2311引用：38难度：0.8

  解析

• 7．一次函数y=ax-b,若a+b=1，则它的图象必经过点（　　）

  A．（-1，-1）

  B．（-1，1）

  C．（1，-1）

  D．（1，1）
  组卷：71引用：2难度：0.7

  解析

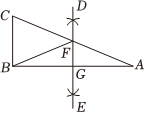• 8．如图，在Rt△ABC中，∠ABC=90°，分别以点A和点B为圆心，大于

  1

  2

  AB的长为半径作弧相交于点D和点E，直线DE交AC于点F，交AB于点G，连接BF，若BF=3，AG=2，则BC=（　　）

  A．5

  B． 4 3

  C． 2 5

  D． 2 13
  组卷：18引用：3难度：0.5

  解析

三、解答题（共62分）

• 24．如图1，对角线互相垂直的四边形叫做垂美四边形．
  
  （1）概念理解：下列三个图形①正方形②菱形③矩形一定是垂美四边形的是

  ；（填序号）
  （2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD，试证明；AB²+CD²=AD²+BC²；
  （3）解决问题：如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结CE、BG、GE．已知AC=3，AB=5，求GE的长．
  组卷：92引用：1难度：0.2

  解析

• 25．如图1，直线AB分别交x轴，y轴于点A（a,0），点B（0，b）且a,b满足a²+4a+4+|2a+b|=0．
  
  （1）a=

  ，b=

  ；
  （2）点P在直线AB的右侧，且∠APB=45°，若△ABP为直角三角形，求点P的坐标；
  （3）如图2，在（2）的条件下，∠BAP=90°且点P在第四象限，AP与y轴交于点M，BP与x轴交于点N，连接MN，求证：∠1=∠2．
  组卷：180引用：1难度：0.5

  解析