2023-2024学年北京市朝阳区陈经纶中学八年级（上）月考数学试卷（9月份）

一、单选题

• 1．如图，用三角板作△ABC的边AB上的高线，下列三角板的摆放位置正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：4696引用：88难度：0.6

  解析

• 2．十二边形的内角和为（　　）

  A．180°

  B．360°

  C．1800°

  D．无法计算
  组卷：274引用：8难度：0.9

  解析

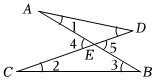• 3．如图，AB和CD相交于点O，则下列结论正确的是（　　）

  A．∠1=∠2

  B．∠5=∠1+∠3

  C．∠4=∠5

  D．∠5＜∠2
  组卷：58引用：3难度：0.5

  解析

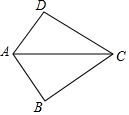• 4．如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）

  A．CB=CD

  B．∠BAC=∠DAC

  C．∠B=∠D=90°

  D．∠BCA=∠DCA
  组卷：4577引用：128难度：0.7

  解析

• 5．下列判定两直角三角形全等的方法，错误的是（　　）

  A．两条直角边对应相等

  B．斜边和一直角边对应相等

  C．两个锐角对应相等

  D．斜边和一锐角对应相等
  组卷：327引用：4难度：0.7

  解析

• 6．根据下列已知条件，能画出唯一的△ABC的是（　　）

  A．∠A=60°，∠B=45°，AB=4	B．∠C=90°，∠B=30°，∠A=60°
  C．AB=3，BC=4，CA=8	D．AB=4，BC=3，∠A=60°
  组卷：187引用：6难度：0.7

  解析

• 7．下列是真命题的是（　　）

  A．对顶角相等

  B．两边和一角对应相等的两个三角形全等

  C．三角形的外角大于内角

  D．两条直线被第三条直线所截，同位角相等
  组卷：69引用：3难度：0.7

  解析

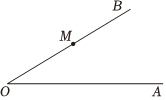• 8．如图，∠AOB＜90°，点M在OB上，且OM=6，点M到射线OA的距离为a,点P在射线OA上，MP=x,若△OMP的形状，大小是唯一确定的，则x的取值范围是（　　）

  A．x=a或x≥6

  B．x≥6

  C．x=6

  D．x=6或x＞a
  组卷：468引用：7难度：0.5

  解析

三、解答题

• 24．【提出问题】
  我们已经知道了三角形全等的判定方法（SAS，ASA，AAS，SSS）和直角三角形全等的判定方法（HL），请你继续对“两边分别相等且其中一组等边的对角相等的两个三角形（SSA）”的情形进行探究．
  【探索研究】
  已知：在△ABC和△DEF中，AB=DE，AC=DF，∠B=∠E．
  （1）如图①，当∠B=∠E=90°时，根据

  ，可知Rt△ABC≌Rt△DEF；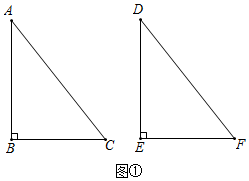
  
  （2）如图②，当∠B=∠E＜90°时，请用直尺和圆规作出△DEF，通过作图，可知△ABC与△DEF

  全等．（填“一定”或“不一定”）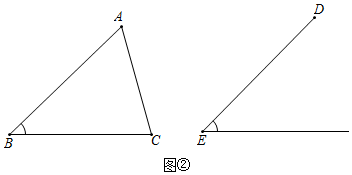
  
  （3）如图③，当∠B=∠E＞90°时，△ABC与△DEF是否全等？若全等，请加以证明：若不全等，请举出反例．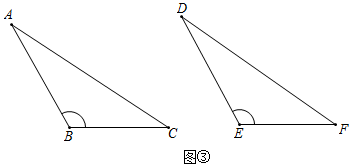
  
  【归纳总结】
  （4）如果两个三角形的两边分别相等且其中一组等边的对角相等，那么当这组对角是

  
  时，这两个三角形一定全等．（填序号）
  ①锐角；②直角；③钝角．
  组卷：503引用：2难度：0.1

  解析

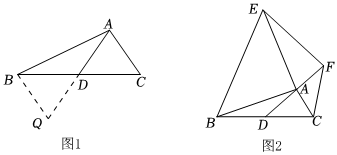• 25．阅读理解：课外兴趣小组活动时，老师提出了如下问题：在△ABC中，AB=7，AC=3，求BC边上的中线AD的取值范围．
  （1）小明在组内经过合作交流，得到了如下的解决方法（如图1）：
  ①延长AD到Q使得DQ=AD；
  ②再连接BQ，把AB、AC、2AD集中在△ABQ中；③利用三角形的三边关系可得4＜AQ＜10，则AD的取值范围是

  ．
  感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
  （2）请写出图1中AC与BQ的位置关系并证明；
  （3）思考：已知，如图2，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°，试探究线段AD与EF的数量和位置关系，并加以证明．
  组卷：887引用：17难度：0.4

  解析