2023-2024学年湖北省天门市七校联考八年级（上）月考数学试卷（9月份）

一、选择题（每题3分，共30分）

• 1．一个三角形的一个内角等于另外两个内角的和，这个三角形是（　　）

  A．直角三角形	B．锐角三角形
  C．钝角三角形	D．何类三角形不能确定
  组卷：449引用：9难度：0.9

  解析

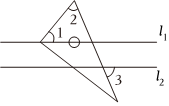• 2．如图，直线l₁∥l₂，∠1=40°，∠2=65°，则∠3=（　　）
  ​

  A．65°

  B．70°

  C．75°

  D．85°
  组卷：37引用：1难度：0.5

  解析

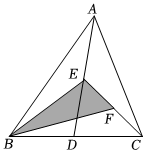• 3．如图，在△ABC中，已知点D，E，F分别为BC，AD，AE的中点，且S_△ABC=8cm²，则阴影部分面积S=（　　）cm²．

  A．1

  B．2

  C．3

  D．4
  组卷：108引用：4难度：0.7

  解析

• 4．若一个正n边形的每个外角为30°，则这个正n边形的边数是（　　）

  A．10

  B．11

  C．12

  D．14
  组卷：494引用：7难度：0.6

  解析

• 5．已知三角形的三边长为3、6、x,则x的取值范围是（　　）

  A．3≤x≤9

  B．3≤x＜9

  C．3＜x≤9

  D．3＜x＜9
  组卷：16引用：2难度：0.7

  解析

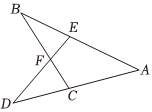• 6．如图，EF=CF，BF=DF，则下列结论错误的是（　　）

  A．△BEF≌△DCF

  B．△ABC≌△ADE

  C．AB=AD

  D．DC=AC
  组卷：294引用：8难度：0.5

  解析

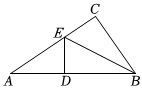• 7．如图，在△ABC中，∠C=90°，ED⊥AB于点D，BD=BC，若AC=6cm,则AE+DE等于（　　）

  A．4cm

  B．5cm

  C．6cm

  D．7cm
  组卷：239引用：3难度：0.7

  解析

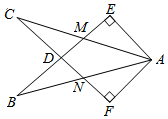• 8．如图，在Rt△AEB和Rt△AFC中，∠E=∠F=90°，BE=CF，BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N，∠EAC=∠FAB．有下列结论：①∠B=∠C；②ED=FD；③AC=BE；④△ACN≌△ABM．其中正确结论的个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：1235引用：11难度：0.5

  解析

三、解答题（共72分）

• 24．问题背景：
  如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．
  小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是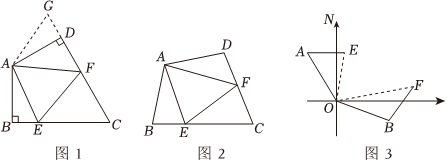

  ；
  
  探索延伸：
  如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠EAF=

  1

  2

  ∠BAD，上述结论是否仍然成立，并说明理由；
  实际应用：
  如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．
  组卷：2471引用：115难度：0.3

  解析

• 25．如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
  （1）如果AB=AC，∠BAC=90°，
  ①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为

  ，线段CF、BD的数量关系为

  ；
  ②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
  （2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．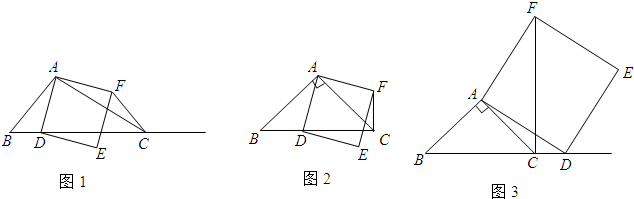
  组卷：490引用：13难度：0.4

  解析