2023-2024学年天津外国语大学附属外国语学校九年级（上）第一次月考数学试卷

一、单选题

• 1．下列方程中是一元二次方程是（　　）

  A． 1 x 2 + x = 2

  B．2x+6=7

  C．x2+y2=5

  D．3x2-5x+2=0
  组卷：322引用：13难度：0.9

  解析

• 2．关于x的方程ax²+bx+c=0是一元二次方程的条件为（　　）

  A．a≠0，b≠0，c≠0	B．a≠0
  C．b≠0	D．c≠0
  组卷：53引用：2难度：0.5

  解析

• 3．已知关于x的一元二次方程x²+px+q=0的两根分别为x₁=2，x₂=-3，则原方程可化为（　　）

  A．（x+2）（x+3）=0	B．（x+2）（x-3）=0
  C．（x-2）（x-3）=0	D．（x-2）（x+3）=0
  组卷：770引用：8难度：0.5

  解析

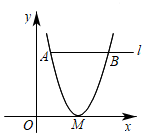• 4．如图，在平面直角坐标系中，抛物线y=（x-h）²与x轴只有一个交点M，与平行于x轴的直线l交于点A、B，若AB=4，则点M到直线l的距离为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：806引用：4难度：0.7

  解析

• 5．二次函数y=x²+ax+b中，若a-b=0，则它的图象必经过点（　　）

  A．（-1，-1）

  B．（1，-1）

  C．（-1，1）

  D．（1，1）
  组卷：158引用：4难度：0.6

  解析

• 6．已知a＜-1，点（a-1，y₁），（a,y₂），（a+1，y₃）都在函数y=x²-2的图象上，则（　　）

  A．y1＜y2＜y3

  B．y1＜y3＜y2

  C．y2＜y1＜y3

  D．y3＜y2＜y1
  组卷：675引用：2难度：0.7

  解析

• 7．抛物线①y=2x²；②y=2（x+1）²-5；③y=3（x+1）²；④y=（x+1）²-5．其中，形状相同的是（　　）

  A．①②

  B．②③④

  C．②④

  D．①④
  组卷：963引用：4难度：0.5

  解析

• 8．青山村种的水稻2014年平均每公顷产8000kg,2016年平均每公顷产9680kg,设该村水稻每公顷产量的年平均增长率为x,根据题意列出方程是（　　）

  A．8000（1+x）2=9680	B．8000（1-x）2=9680
  C．9680（1+x）2=8000	D．9680（1-x）2=8000
  组卷：179引用：7难度：0.7

  解析

• 9．一元二次方程x²-8x-1=0配方后可变形为（　　）

  A．（x+4）2=17

  B．（x+4）2=15

  C．（x-4）2=17

  D．（x-4）2=15
  组卷：518引用：28难度：0.6

  解析

• 10．设a,b是方程x²+x-2019=0的两个实数根，则a+b+ab的值为（　　）

  A．2018

  B．-2018

  C．2020

  D．-2020
  组卷：735引用：9难度：0.6

  解析

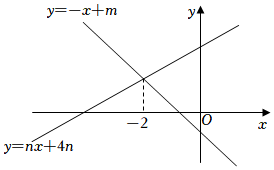• 11．如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2．则下列结论：
  ①m＜0，n＞0；
  ②直线y=nx+4n一定经过点（-4，0）；
  ③m与n满足m=2n-2；
  ④不等式-x+m＞nx+4n＞0的解集为x＜-2，
  其中正确结论的个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：1086引用：5难度：0.5

  解析

三、解答题

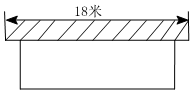• 33．如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m,设垂直于墙的一边长为x米．
  （1）当x为何值时，菜园的面积为100m²；
  （2）当x为何值时，菜园的面积最大？最大面积是多少？
  组卷：247引用：6难度：0.6

  解析

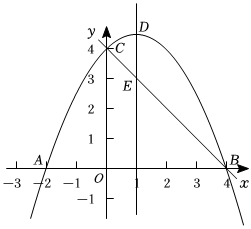• 34．如图，抛物线y=ax²+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（-2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．
  （1）求抛物线的解析式；
  （2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积最大，若存在，求出点F的坐标和最大值；若不存在，请说明理由；
  （3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求P点的坐标．
  （4）探究对称轴上是否存在一点P，使得以点P，C，A为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的P点的坐标，若不存在，请说明理由．
  组卷：647引用：3难度：0.1

  解析