2022-2023学年江苏省无锡市新吴区辅仁高级中学高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若z（1-i）=（1+i）²，则在复平面内复数z对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：59引用：1难度：0.8

  解析

• 2．两个粒子A，B从同一发射源发射出来，在某一时刻，它们的位移分别为

  s

  A

  =

  （

  4

  ，

  3

  ）

  ，

  s

  B

  =

  （

  -

  2

  ，

  6

  ）

  ，则

  s

  B

  在

  s

  A

  上的投影向量的长度为（　　）

  A．10

  B． 10 2

  C． 10 10

  D．2
  组卷：201引用：4难度：0.7

  解析

• 3．若一个样本容量为8的样本的平均数为5，方差为2．现样本中又加入一个新数据5，此时样本容量为9，平均数为

  x

  ，方差为s²，则（　　）

  A． x = 5 ，s2＞2

  B． x = 5 ，s2＜2

  C． x ＞ 5 ，s2＜2

  D． x ＞ 5 ，s2＞2
  组卷：247引用：2难度：0.9

  解析

• 4．抛掷两枚质地均匀的硬币，设事件A=“第一枚硬币正面朝上”，B=“第二枚硬币反面朝上”（　　）

  A．A与B互为对立事件	B．A与B互斥
  C．A与B相等	D．P（A）=P（B）
  组卷：215引用：3难度：0.6

  解析

• 5．四棱台ABCD-EFGH中，其上、下底面均为正方形，若EF=2AB=8，且每条侧棱与底面所成角的正切值均为

  3

  2

  ，则该棱台的体积为（　　）

  A．224

  B．448

  C． 224 3

  D．147
  组卷：154引用：2难度：0.5

  解析

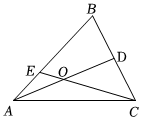• 6．如图，在△ABC中，点D为BC边的中点，O为线段AD的中点，连接CO并延长交AB于点E，设

  AB

  =

  a

  ，

  AC

  =

  b

  ，则

  CE

  =（　　）

  A． 1 4 a - 3 4 b

  B． 1 4 a - b

  C． 1 3 a - b

  D． 1 3 a - 3 4 b
  组卷：181引用：3难度：0.7

  解析

• 7．在△ABC中，CD为角C的平分线，若B=2A，3AD=4BD，则cosA等于（　　）

  A．0

  B． 1 2

  C． 2 3

  D． 3 4
  组卷：216引用：5难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤.

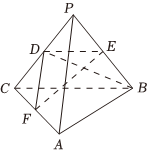• 21．如图，在三棱锥P-ABC中，平面PBC⊥平面ABC，△PBC为等边三角形，D，E分别为PC，PB的中点，BD⊥PA，BC=2，AC=1．
  （1）求证：AC⊥平面PBC；
  （2）在线段AC上是否存在点F，使得平面DEF与平面ABC的夹角为

  π

  3

  ，若存在，求出CF的长；若不存在，请说明理由．
  组卷：426引用：5难度：0.4

  解析

• 22．记△ABC的内角A，B，C的对边分别为a,b,c,已知

  a

  2

  -

  b

  2

  c

  2

  =

  a

  2

  +

  b

  2

  -

  c

  2

  ab

  ．
  （1）若C=

  π

  4

  ，求A，B；
  （2）若△ABC为锐角三角形，求

  a

  b

  cos

  2

  B

  的取值范围．
  组卷：762引用：5难度：0.6

  解析