当前位置：试卷中心 > 试卷详情

2023-2024学年广西柳州市柳江区九年级（上）期中数学试卷

发布：2024/10/1 0:0:2

一、单选题（12小题，每题3分，共36分）

1．下列方程中，是一元二次方程的是（　　）
A．x²+
1
x
=0 B．x²+xy+1=0 C．3x+2=1 D．x²=1
组卷：265引用：6难度：0.7
解析
2．抛物线y=-（x-2）²+1的对称轴为（　　）
A．直线x=1 B．直线x=2 C．直线x=-1 D．直线x=-2
组卷：71引用：3难度：0.6
解析
3．下列分别是回收、低碳、节水、节能的四个标志，其中是中心对称图形的是（　　）
A． B． C． D．
组卷：73引用：7难度：0.9
解析
4．在一个边长为2的正方形中挖去一个边长为x（0＜x＜2）的小正方形，如果设剩余部分的面积为y,那么y关于x的函数解析式是（　　）
A．y=x² B．y=4-x² C．y=x²-4 D．y=4-2x
组卷：980引用：6难度：0.7
解析
5．下列各点中，是二次函数y=x²-2图象上的点是（　　）
A．（1，3） B．（0，0） C．（2，1） D．（0，-2）
组卷：57引用：6难度：0.5
解析
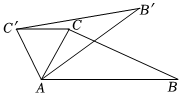6．如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC'∥AB，划∠BAB′的度数是（　　）
A．35° B．40° C．50° D．70°
组卷：447引用：11难度：0.7
解析
7．如果关于x的一元二次方程kx²-6x+9=0有两个不相等的实数根，那么k的取值范围是（　　）
A．k＜1 B．k≠0 C．k＜1且k≠0 D．k＞1
组卷：1791引用：132难度：0.9
解析
8．把一元二次方程x²+12x+27=0化为（x+p）²=q的形式，正确的是（　　）
A．（x-6）²=9 B．（x+6）²=9
C．（x+12）²=-27 D．（x+6）²=-27
组卷：36引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（8小题，共72分）

25．如图1，在边长为4的正方形ABCD中，连接AC，点E在BC上，且BE=EC，将点C绕点B逆时针旋转至点F，旋转角的度数为α，连接BF，与AC相交于点G，连接EF，交AC于点H，当点C旋转到与点A重合时旋转停止．

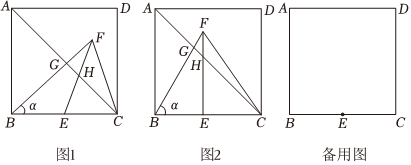
（1）如图2，当α=60°时，
①求证：EF⊥BC；
②点H在线段AC的什么位置？请说明理由；
（2）在旋转的过程中，是否存在△CEF为等腰三角形的情况？如果存在，请直接写出EF的长；如果不存在，请说明理由．
组卷：78引用：5难度：0.5
解析
26．2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情，如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线
C
1
：
y
=
-
1
12
x
2
+
7
6
x
+
1
近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线
C
2
：
y
=
-
1
8
x
2
+
bx
+
c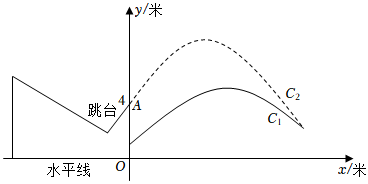
运动．

（1）当运动员运动到离A处的水平距离为4米时，离水平线的高度为8米，求抛物线C₂的函数解析式（不要求写出自变量x的取值范围）；
（2）在（1）的条件下，当运动员运动的水平距离为多少米时，运动员与小山坡的竖直距离为1米？
（3）当运动员运动到坡顶正上方，且与坡顶距离超过3米时，请直接写出b的取值范围．
组卷：761引用：6难度：0.5
解析