人教新版八年级上册《第12章 全等三角形》2023年单元测试卷（14）
发布：2024/9/15 10:0:8
一、选择题
-
1．如图所示，△ABC≌△ECD，∠A=48°，∠D=62°，则图中∠B的度数是（ ）组卷：201引用：3难度：0.8 -
2．下列条件中，能判定两个直角三角形全等的是（ ）
组卷：4304引用：84难度：0.9 -
3．如图，a,b,c为△ABC的三边长，则甲、乙、丙三个三角形中和△ABC全等的是（ ）
组卷：152引用：3难度：0.6 -
4．如图，在△ABC中，∠C=90°，AC=8，3DC=AD，BD平分∠ABC，则点D到AB的距离等于（ ）组卷：1169引用：14难度：0.5 -
5．如图，N，C，A三点在同一直线上，在△ABC中，∠A：∠ABC：∠ACB=3：5：10，又△MNC≌△ABC，则∠BCM：∠BCN等于（ ）组卷：7442引用：34难度：0.5 -
6．如图，△ABC的三边AB，BC，CA的长分别为20，30，20，三条角平分线交于点O，则S△ABO：S△BOC：S△CAO等于（ ）组卷：266引用：2难度：0.6 -
7．如图所示，已知OA=OB，OC=OD，AD、BC相交于点E，则图中全等三角形共有（ ）组卷：904引用：13难度：0.9 -
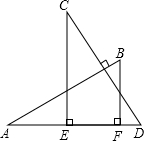8．如图，AB⊥CD，且AB=CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE=5，BF=3，EF=2，则AD的长为（ ）组卷：1412引用：6难度：0.7
三、解答题
-
23．如图①，AM∥BN，AE平分∠BAM，BE平分∠ABN．
（1）求∠AEB的度数；
（2）如图②，过点E的直线交射线AM于点C，交射线BN于点D．求证：AC+BD=AB．
组卷：635引用：3难度：0.5 -
24．（1）如图①，已知：△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥m于D，CE⊥m于E，求证：DE=BD+CE；
（2）拓展：如图②，将（1）中的条件改为：△ABC中，AB=AC，D、A、E三点都在直线m上，并且∠BDA=∠AEC=∠BAC=α，α为任意锐角或钝角，请问结论DE=BD+CE是否成立？如成立，请证明；若不成立，请说明理由；
（3）应用：如图③，在△ABC中，∠BAC是钝角，AB=AC，∠BAD＞∠CAE，∠BDA=∠AEC=∠BAC，直线m与BC的延长线交于点F，若BC=2CF，△ABC的面积是16，求△ABD与△CEF的面积之和．
组卷：1469引用：8难度：0.7
