2021年山西省晋中市榆次区中考数学一模试卷

一、选择题（本大题共10个小题，每小题3分，共30分，在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）

• 1．有理数-2的相反数是（　　）

  A．2

  B． 1 2

  C．-2

  D．- 1 2
  组卷：1024引用：31难度：0.9

  解析

• 2．观看央视春晚是大部分华人除夕夜的“标配”，截至今年除夕夜24时，2021年春晚海内外受众总规模再创新高，达12.72亿人，且连续第三年刷新跨媒体传播记录．其中数据12.72亿用科学记数法表示为（　　）

  A．1.272×1011

  B．1.272×1010

  C．1.272×109

  D．1.272×108
  组卷：11引用：1难度：0.9

  解析

• 3．下列运算正确的是（　　）

  A．m2+m2=2m4	B．m2•m4=m6
  C．（-3m2n）2=-9m5n3	D．（m+n）2=m2+n2
  组卷：30引用：2难度：0.7

  解析

• 4．如图所示的几何体是由9个大小相同的小正方体组成的，将小正方体①移走后，所得几何体的三视图没有发生变化的是（　　）

  A．主视图和左视图	B．主视图和俯视图
  C．左视图和俯视图	D．主视图、左视图、俯视图
  组卷：1368引用：20难度：0.9

  解析

• 5．国际数学教育大会是全球数学教育界水平最高、规模最大的学术会议，第14届国际数学教育大会（1CME-14）将于2021年7月在上海举办，这是我国第一次承办此项大会．如图是这次大会的会标，会标蕴含了丰富的数学元素，其中会标中心的弦图是三国时期一位数学家所给出勾股定理的一个绝妙证法．这位数学家是（　　）

  A．欧几里得

  B．杨辉

  C．祖冲之

  D．赵爽
  组卷：36引用：1难度：0.9

  解析

• 6．某班有50人，一次体能测试后，老师对测试成绩进行了统计．由于小亮没有参加本次集体测试，因此计算其他49人的平均分为90分，方差s²=41．后来小亮进行了补测，成绩为90分，关于该班50人的测试成绩，下列说法正确的是（　　）

  A．平均分不变，方差变大	B．平均分不变，方差变小
  C．平均分和方差都不变	D．平均分和方差都改变
  组卷：14引用：1难度：0.7

  解析

• 7．解不等式组

  3 - x ≤ 4 ①

  2 3 x + 1 ＞ x - 2 3 ②

  时，不等式①②的解集在同一条数轴上表示正确的是（　　）

  A．	B．
  C．	D．
  组卷：146引用：1难度：0.6

  解析

三、解答题（本大题含8个小题，共75分，解答题应写出文字说明，证明过程或演算步骤）

• 22．综合与实践
  问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在正方形ABCD中，点E是边BC的中点，以点E为直角顶点，DE为直角边作Rt△DEF，且ED=EF，DF交边AB于点M，过点F作FG⊥AB于点G．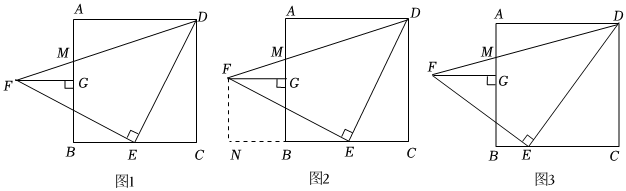
  ​
  操作发现：
  （1）勤奋小组：过点F作FN⊥BC，交CB的延长线于点N（如图2），发现△FNE≌△ECD．请你写出证明过程；
  （2）求实小组：受勤奋小组的启发，发现线段FG与BG之间存在某种数量关系，请你写出它们之间的数量关系，并证明；
  拓广探索：
  （3）创新小组：受勤奋小组和求实小组的启发，继续进行探究，如图3，在正方形ABCD中，点E是边BC的四等分点，BE=

  1

  4

  BC，以点E为直角顶点，DE为直角边作Rt△DEF，且∠EDF=30°，DF交边AB于点M，过点F作FG⊥AB于点G．线段FG与BG之间存在怎样的数量关系？请你直接写出结论．
  组卷：74引用：1难度：0.5

  解析

• 23．综合与探究
  如图，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C（0，-3），顶点为D（h,-4），点E（-1，-2）在抛物线对称轴上．若点P是第三象限内抛物线上一动点．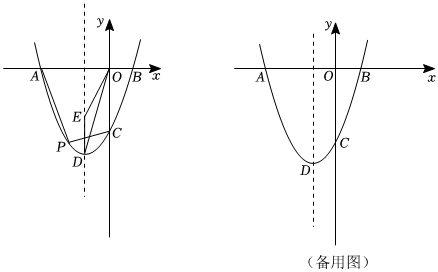
  ​
  （1）求抛物线的表达式；
  （2）当S_△ACP=3S_△ODE时，求点P的坐标；
  （3）若点M为抛物线对称轴上一点，平面内是否存在点N，使得以C、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．
  组卷：46引用：1难度：0.5

  解析