2020-2021学年安徽省宿州市泗县一中高一（下）第三次月考数学试卷

一、选择题（共12题，每题5分）

• 1．若复数

  z

  =

  2

  -

  i

  1

  +

  i

  ，则z在复平面内所对应的点位于的（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：155引用：5难度：0.9

  解析

• 2．已知在△ABC中，角A，B，C所对的边分别为a,b,c,且a=x,b=3，B=45°．若此三角形有两解，则实数x的取值范围是（　　）

  A．x＞3

  B． 3 ＜ x ＜ 3 2

  C． 3 ＜ x ＜ 2 3

  D．0＜x＜3
  组卷：105引用：3难度：0.7

  解析

• 3．过球面上任意两点A，B作大圆，可能的个数是（　　）

  A．有且只有一个	B．一个或无数个
  C．无数个	D．以上均不正确
  组卷：58引用：4难度：0.8

  解析

• 4．已知α，β均为锐角，cos（α+β）=-

  5

  13

  ，sin（β+

  π

  3

  ）=

  3

  5

  ，则cos（α+

  π

  6

  ）=（　　）

  A． 33 65

  B． 63 65

  C．- 33 65

  D．- 63 65
  组卷：652引用：11难度：0.9

  解析

• 5．设△ABC的三个内角A，B，C，向量

  m

  =

  （

  3

  sin

  A

  ，

  sin

  B

  ）

  ，

  n

  =

  （

  cos

  B

  ，

  3

  cos

  A

  ）

  ，若

  m

  •

  n

  =1+cos（A+B），则C=（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：1075引用：41难度：0.9

  解析

• 6．A，B分别是复数z₁，z₂在复平面内对应的点，O是坐标原点，若|z₁+z₂|=|z₁-z₂|，则△AOB一定是（　　）

  A．等腰三角形	B．直角三角形
  C．等边三角形	D．等腰直角三角形
  组卷：128引用：3难度：0.8

  解析

• 7．下列说法中，正确的个数为（　　）
  （Ⅰ）有一个面是多边形，其余各面都是三角形的几何体是棱锥；
  （Ⅱ）有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台；
  （Ⅲ）底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
  （Ⅳ）棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是正六棱锥．

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：356引用：2难度：0.6

  解析

三、解答题（共六题，70分）

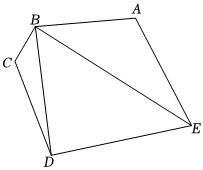• 21．杭州市为迎接2022年亚运会，规划修建公路自行车比赛赛道，该赛道的平面示意图为如图的五边形ABCDE，运动员的公路自行车比赛中如出现故障，可以从本队的器材车、公共器材车上或收容车上获得帮助．比赛期间，修理或更换车轮或赛车等，也可在固定修车点上进行，还需要运送一些补给物品，例如食物、饮料，工具和配件．所以项目设计需要预留出BD，BE为赛道内的两条服务通道（不考虑宽度），ED，DC，CB，BA，AE为赛道，∠BCD=∠BAE=

  2

  π

  3

  ，∠CBD=

  π

  4

  ，CD=

  6

  km,DE=4km.
  （1）从以下两个条件中任选一个条件，求服务通道BE的长度；
  ①∠CDE=

  7

  π

  12

  ；②cos∠DBE=

  3

  5

  ；
  （2）在（1）条件下，应该如何设计，才能使折线段赛道BAE最长（即BA+AE最大），最长为多少？
  组卷：51引用：4难度：0.6

  解析

• 22．如图，在扇形OAB中，∠AOB=120°，半径OA=OB=4，P为弧AB上一点（含端点）．
  （1）若OB⊥OP，

  OP

  =

  λ

  OA

  +

  μ

  OB

  ，求λ，μ的值；
  （2）求

  PA

  •

  PB

  的最小值．
  组卷：18引用：1难度：0.5

  解析