2022-2023学年安徽省芜湖市无为市襄安中学九年级（上）期中数学试卷

一．选择题（共10小题，满分40分，每小题4分）

• 1．下列方程，是一元二次方程的是（　　）

  A． x 2 - 1 x = 1	B．3x2+x=20
  C．2x2-3xy+4=0	D．ax2+bx+c=0
  组卷：108引用：13难度：0.8

  解析

• 2．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：35引用：1难度：0.5

  解析

• 3．用配方法解一元二次方程：x²-4x-2=0，可将方程变形为（x-2）²=n的形式，则n的值是（　　）

  A．0

  B．2

  C．4

  D．6
  组卷：403引用：7难度：0.7

  解析

• 4．在平面直角坐标系中，将抛物线y=-5x²+3向左平移1个单位，再向下平移1个单位后所得抛物线的表达式为（　　）

  A．y=-5（x+1）2+2	B．y=-5（x+1）2+4
  C．y=-5（x-1）2+2	D．y=-5（x-1）2+4
  组卷：374引用：4难度：0.6

  解析

• 5．一种药品经过两次降价，药价从每盒60元下调至48.6元，若平均每次降价的百分率为x,则可列方程为（　　）

  A．60（1+x）=48.6	B．60（1-x）=48.6
  C．60（1+x）2=48.6	D．60（1-x）2=48.6
  组卷：464引用：5难度：0.8

  解析

• 6．若点A（a-2，3）和（-1，b+2）关于原点对称，则（a,b）在第几象限（　　）

  A．第二象限

  B．第一象限

  C．第四象限

  D．第三象限
  组卷：112引用：2难度：0.9

  解析

• 7．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=2，∠B=60°，则CD的长为（　　）

  A．1

  B． 3

  C．2

  D．2 2
  组卷：85引用：4难度：0.6

  解析

三．解答题（共9小题，满分90分）

• 22．某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价为25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．
  （1）写出每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；并求当x为多少时，w有最大值，最大值是多少？
  （2）商场的营销部结合上述情况，提出了甲、乙两种营销方案：方案甲：该文具的销售单价高于进价且不超过30元；方案乙：每天销售量不少于10件，且每件文具的利润至少为25元．
  请比较哪种方案的最大利润更高，并说明理由．
  组卷：740引用：2难度：0.3

  解析

• 23．已知△AOB和△MON都是等腰直角三角形（

  2

  2

  OA＜OM＜OA），∠AOB=∠MON=90°．
  （1）如图1，连接AM，BN，求证：AM=BN；
  （2）将△MON绕点O顺时针旋转．
  ①如图2，当点M恰好落在AB边上时，求证：AM²+BM²=2OM²；
  ②当点A，M，N在同一条直线上时，若OA=4，OM=3，请直接写出线段AM的长．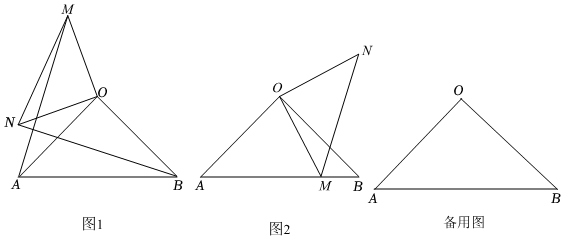
  
  组卷：720引用：3难度：0.1

  解析