2022-2023学年广西桂林市八年级（下）期末数学试卷
发布：2024/6/30 8:0:9
一、选择题（共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）
-
1．已知：点P的坐标为（-2，1），则点P所在的象限是（ ）
组卷：120引用：4难度：0.9 -
2．下面图形中，是中心对称图形的是（ ）
组卷：8引用：1难度：0.9 -
3．我们把每一组数的频数与数据总数的比叫作这一组数据的频率（relative frequency）．在“relative”中，字母“e”出现的频率是（ ）
组卷：52引用：2难度：0.7 -
4．由线段a,b,c组成的三角形是直角三角形的是（ ）
组卷：54引用：5难度：0.5 -
5．下列各点，在函数y=x+2的图象上的是（ ）
组卷：32引用：2难度：0.7 -
6．在一个凸多n边形中，它的内角和是540°，则n为（ ）
组卷：251引用：3难度：0.7 -
7．菱形的两条对角线的长分别是6和8，则这个菱形的面积是（ ）
组卷：166引用：4难度：0.6 -
8．将直线y=2x-1向上平移3个单位，可得到直线（ ）
组卷：80引用：2难度：0.7
三、解答题（本大题共8题，共72分，请将解答过程写在答题卡上）
-
25．综合与实践
在学了《四边形》一章后，老师让同学们以“矩形的折叠”为主题开展数学活动．
【操作发现】某活动小组准备了一张矩形纸片，进行如下操作：将矩形纸片ABCD对折，点A与点D重合，点B与点C重合，折痕为MN，点P是DC边上的任意一点，沿MP和NP剪掉两个角，展开后得到四边形PNQM，如图1．
（1）通过观察，发现四边形PNQM是一类特殊的四边形，请你写出这类特殊四边形的边角特征（用几何语言表述，至少写出两个）；
【深入探究】小组成员通过查阅资料，了解到我们通常把具有以上特征的四边形叫做“筝形”，同时还了解到筝形的一条对角线垂直平分另一条对角线．
（2）如图2，在四边形PNQM中，若MP=MQ，NP=NQ，则MN⊥PQ，且MN平分PQ，请证明这个结论；
【拓展应用】
（3）如图3，在筝形PNQM中，∠PMQ=60°，NE∥MP交MQ于点E，若NE=6，求MN的长．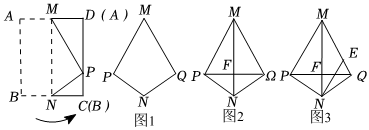
组卷：112引用：1难度：0.3 -
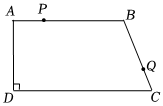26．如图，在四边形ABCD中，AB∥CD，∠ADC=90°，AD=12cm,AB=18cm,CD=23cm,动点P从点A出发，以1cm/s的速度向终点B运动，同时动点Q从点B出发，以2cm/s的速度沿折线B-C-D向终点D运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．
（1）用含t的式子表示PB．
（2）当t为何值时，直线PQ把四边形ABCD分成两个部分，且其中的一部分是平行四边形？
（3）只改变点Q的运动速度，使运动过程中某一时刻四边形PBCQ为菱形，则点Q的运动速度应为多少？组卷：1346引用：5难度：0.3
