2020-2021学年广东省广州市番禺区祈福英语实验学校九年级（上）月考数学试卷（12月份）

一、选择题（共十题：共30分）

• 1．点P（4，-3）关于原点的对称点是（　　）

  A．（4，3）

  B．（-3，4）

  C．（-4，3）

  D．（3，-4）
  组卷：750引用：17难度：0.9

  解析

• 2．已知x=2是关于x的一元二次方程x²-x-2a=0的一个解，则a的值为（　　）

  A．0

  B．1

  C．-1

  D．2
  组卷：10引用：3难度：0.7

  解析

• 3．如图，在△ABC中，∠C=90°，点D在CB上，DE⊥AB，若DE=2，CA=4，则

  DB

  AB

  =（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  组卷：293引用：7难度：0.9

  解析

• 4．正六边形的边心距为

  3

  ，则该正六边形的边长是（　　）

  A． 3

  B．2

  C．3

  D．2 3
  组卷：2364引用：65难度：0.9

  解析

• 5．由二次函数y=2（x-3）²+1，可知（　　）

  A．其图象的开口向下

  B．其图象的对称轴为直线x=-3

  C．其最小值为1

  D．当x＜3时，y随x的增大而增大
  组卷：1818引用：141难度：0.9

  解析

• 6．如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为

  1

  3

  ，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（　　）

  A．（2，1）

  B．（2，0）

  C．（3，3）

  D．（3，1）
  组卷：4751引用：117难度：0.9

  解析

• 7．如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则△BCF的面积为（　　）

  A．S

  B．2S

  C．3S

  D．4S
  组卷：80引用：4难度：0.9

  解析

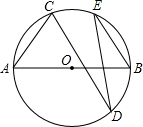• 8．如图，AB为⊙O的直径，∠BED=40°，则∠ACD的度数为（　　）

  A．90°

  B．50°

  C．45°

  D．80°
  组卷：1070引用：13难度：0.7

  解析

三、解答题（共九题：共72分）

• 24．如图，在半径为2的⊙O中，AB是直径，M是弧AB的中点，OC⊥OD，△COD绕点O旋转与△AMB的两边分别交于E、F（点E、F与点A、B、M均不重合），与⊙O分别交于P、Q两点．
  
  （1）连接OM，求证：△OBE≌△OMF．
  （2）连接PM、QM，试探究；在△COD绕点O旋转的过程中，∠PMQ是否为定值？若是，求出∠PMQ的大小；若不是，请说明理由．
  （3）连接EF，试探究：在△COD绕点O旋转的过程中，△EFM的周长是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．
  组卷：25引用：2难度：0.5

  解析

• 25．在平面直角坐标系中，抛物线y=x²+（k-1）x-k与直线y=kx+1交于A，B两点，点A在点B的左侧．
  （1）如图1，当k=1时，直接写出A，B两点的坐标；
  （2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
  （3）如图2，抛物线y=x²+（k-1）x-k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），在直线y=kx+1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由．
  
  组卷：6570引用：72难度：0.1

  解析