2023-2024学年山东省淄博市张店区七年级（上）期中数学试卷（五四学制）

一、选择题（本题共10小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填涂在答题纸的相应位置上）

• 1．如图图形中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：62引用：8难度：0.9

  解析

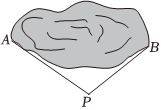• 2．如图，为估计池塘两岸A，B间的距离，小杨在池塘一侧选取了一点P，测得PA=26m,PB=14m,那么AB之间的距离可能是（　　）

  A．40m

  B．32m

  C．12m

  D．10m
  组卷：59引用：2难度：0.7

  解析

• 3．如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（　　）
  

  A．

  B．

  C．

  D．
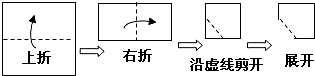  组卷：1587引用：61难度：0.9

  解析

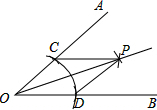• 4．尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于

  1

  2

  CD长为半径画弧，两弧交于点P，作射线OP．由作法得△OCP≌△ODP的根据是（　　）

  A．SAS

  B．ASA

  C．AAS

  D．SSS
  组卷：1257引用：72难度：0.9

  解析

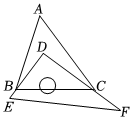• 5．如图，将三角板DEF的直角放置在△ABC内，恰好三角板的两条直角边分别经过点B，C．若∠A=55°，则∠ABD+∠ACD=（　　）

  A．35°

  B．45°

  C．55°

  D．60°
  组卷：688引用：4难度：0.5

  解析

• 6．利用尺规作△ABC，根据下列条件作出的△ABC不唯一的是（　　）

  A．AB=7，AC=5，∠A=60°	B．AC=5，∠A=60°，∠C=80°
  C．AB=7，AC=5，∠B=30°	D．AB=7，BC=6，AC=5
  组卷：103引用：2难度：0.7

  解析

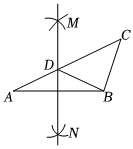• 7．在△ABC中，按以下步骤作图：①分别以A，B为圆心，大于

  1

  2

  AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若CD=BC，∠A=35°，则∠C=（　　）

  A．40°

  B．50°

  C．60°

  D．70°
  组卷：1018引用：6难度：0.9

  解析

三、解答题（本题共8小题，请把解答过程写在答题纸上）

• 22．数学兴趣小组在活动时，老师提出了这样一个问题：
  如图1，在△ABC中，AB=6，AC=10，D是BC的中点，求BC边上的中线AD的取值范围．
  【阅读理解】
  小明在组内经过合作交流，得到了如下的解决方法：
  （1）如图1，延长AD到点E，使DE=AD，连接BE．根据

  可以判定△ADC≌

  ，得出AC=

  ．
  这样就能把线段AB，AC，2AD集中在△ABE中．利用三角形三边的关系，即可得出中线AD的取值范围是

  ．
  【方法感悟】
  当条件中出现“中点”，“中线”等条件时，可以考虑作“辅助线”——把中线延长一倍，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中，这种作辅助线的方法称为“中线加倍”法．
  【问题解决】
  （2）如图2，在△ABC中，∠A=90°，D是BC边的中点，∠EDF=90°，DE交AB于点E，DF交AC于点F，连接EF．请判断BE，CF，EF的数量关系，并说明理由．
  【问题拓展】
  （3）如图3，△ABC中，∠B=90°，AB=3，AD是△ABC的中线，CE⊥BC，CE=5，且∠ADE=90°，请直接写出AE的长．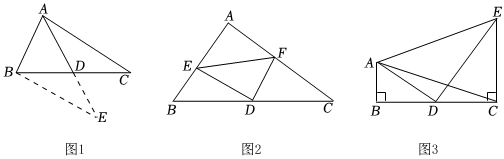
  
  组卷：457引用：2难度：0.1

  解析

• 23．（1）如图1，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE．说明BD=CE的理由；
  （2）如图2，在△ACB和△DCE中，AC=BC，DC=EC，∠ACB=∠DCE=60°，点A，D，E在同一直线上，连接BE．直接写结论：∠AEB=

  °；
  （3）如图3，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，AC=BC，DC=EC，点A，D，E在同一直线上，CM为△DCE的边DE上的高，连接BE．已知CM=2，△BEC的面积为3（即S_△BEC=3），请求出△ACB的面积．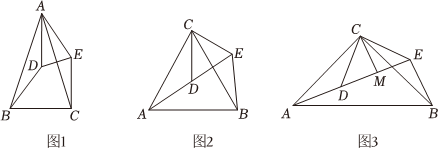
  
  组卷：253引用：1难度：0.3

  解析