当前位置：试卷中心 > 试卷详情

2014年第十届“IMC国际数学竞赛”中国赛区初赛试卷（六年级）

发布：2024/8/21 0:0:1

1．计算：
4
1
2
-
1
3
+
5
1
2
+
1
3
+
6
1
3
-
1
4
+
7
1
3
+
1
4
=
。
组卷：32引用：1难度：0.7
解析
2．大家知道“斐波那契数列”的规律是从第三项起，每一项等于前两项之和，a₁=1，a₂=1，a₃=2，a₄=3，a₅=5，a₆=8，…，那么
a
2
a
1
×
a
3
+
a
4
a
3
×
a
5
+
a
6
a
5
×
a
7
+
a
8
a
7
×
a
9
+
a
10
a
9
×
a
11
=
。
组卷：75引用：1难度：0.6
解析
3．将2014个棱长为1cm的小正方体，搭建成由一个正方体和一个长方体组成的实心模型（如图），已知正方体棱长为10cm,长方体的底面为正方形，那么这个立体模型的表面积为
cm²。
组卷：60引用：1难度：0.5
解析
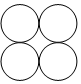4．图中给出了4个半径为10cm的圆紧靠在一起，4个圆的圆心恰好是正方形的四个顶点，那么如果在中心空缺处再画一个圆，则面积为
cm²。（已知正方形的对角线约为边长的1.4倍，π=3.14）
组卷：11引用：1难度：0.8
解析
5．用数字1～9各一次组成若干个整数，如果要求这些整数都是合数（例如：1345、27、96、8），这些合数之和的最小值为
。
组卷：5引用：1难度：0.5
解析

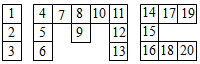14．如图，用小正方形拼成“IMC”的形状，甲、乙两人轮流从中涂黑一个1×2的小长方形（方格不能重复涂黑），轮到谁无法按要求涂黑时，就算谁输。甲为了保证获胜，应该先涂黑标有
和
的长方形。
组卷：12引用：1难度：0.8
解析
15．有十匹赛马编号为A₁～A₁₀，它们的实力排名分别为A₁＞A₂＞A₃＞…＞A₉＞A₁₀，实力靠前的赛马必定能胜实力靠后的赛马。现在安排一次比赛，每场比赛让两匹赛马PK，每匹赛马恰好比赛3场，胜2场即可被评为“骏马”，那么合理安排比赛，最多可以使
匹赛马被评为“骏马”。
组卷：4引用：1难度：0.5
解析

1．计算：412-13+512+13+613-14+713+14=。