2022-2023学年广东省惠州市惠阳区星湖中学七年级（上）月考数学试卷（12月份）
发布：2024/9/6 7:0:8
一、选择题：本大题共10小题，每小题3分，共30分。
-
1．深圳地铁14号线全长约50340m,那么这个数用科学记数法表示为（ ）
组卷：16引用：3难度：0.9 -
2．若∠α和∠β互余，且∠α：∠β=7：2，则∠α为（ ）
组卷：23引用：2难度：0.8 -
3．x表示一个两位数，把3写到x的右边组成一个三位数，则表示这个三位数的代数式是（ ）
组卷：335引用：9难度：0.7 -
4．有理数a、b、c在数轴上的位置如图所示，则式子|a|+|b|+|a+b|-|b-c|化简结果为（ ）组卷：951引用：6难度：0.6 -
5．如图，数轴上点A，B，C所对应的数分别为a,b,c,且都不为0，点C是线段AB的中点，若|a+b|=|a+b+2c|+|b-2c|-|a-2c|，则原点O的位置（ ）组卷：407引用：7难度：0.7 -
6．某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：
方案一，第一次提价10%第二次提价30%；
方案二，第一次提价30%，第二次提价10%；
方案三，第一、二次提价均为20%．三种方案哪种提价最多（ ）组卷：1207引用：5难度：0.6 -
7．若关于x的一元一次方程4x+m+1=3x-1的解是负数，则m的取值范围是（ ）
组卷：59引用：2难度：0.5 -
8．手工课上，老师将同学们分成A，B两个小组制作两个汽车模型，每个模型先由A组同学完成打磨工作，再由B组同学进行组装完成制作，两个模型每道工序所需时间如下：
则这两个模型都制作完成所需的最短时间为（ ）min.模型 打磨/min 组装/min 模型甲 9 5 模型乙 6 11 组卷：6引用：1难度：0.6
三、解答题：本大题共8小题，第18、19小题6分，第20、21小题7分，第22、23小题8分，第24、25小题10分
-
24．A、B、C为数轴上的三点，动点A、B同时从原点出发，动点A每秒运动x个单位，动点B每秒运动y个单位，且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8．
（1）若2秒后，a、b满足|a+8|+（b-2）2=0，则x=，y=，并请在数轴上标出A、B两点的位置．
（2）若动点A、B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后使得|a|=|b|，使得z=．
（3）若动点A、B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，点A与点B之间的距离为AB，且AC+BC=1.5AB，则t=．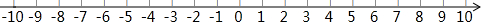
组卷：662引用：6难度：0.5 -
25．阅读理解：如图，A、B、C为数轴上三点，若点C到A的距离是点C到B的距离的2倍，我们就称点C是[A，B]的好点．例如，如图1，点A表示的数为-1，点B表示的数为2．表示数1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的好点；又如，表示数0的点D到点A的距离是1，到点B的距离是2，那么点D就不是[A，B]的好点，但点D是[B，A]的好点．
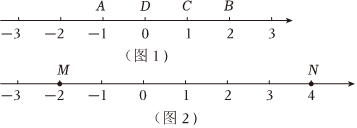
知识运用：如图2，M、N为数轴上两点，点M所表示的数为-2，点N所表示的数为4．
（1）数 所表示的点是[M，N]的好点；
（2）现有一只电子蚂蚁P从点N出发，以每秒2个单位的速度沿数轴向左运动，运动时间为t.当t为何值时，P、M、N中恰有一个点为其余两点的好点？组卷：2219引用：11难度：0.3
