2020-2021学年山东省淄博市张店区东方双语学校八年级（上）月考数学试卷（9月份）

一、单项选择题（共十二题：共36分）

• 1．下列四种垃圾分类回收标识中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：362引用：6难度：0.9

  解析

• 2．在△ABC中，画出边AC上的高，下面4幅图中画法正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：3423引用：23难度：0.9

  解析

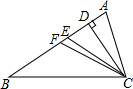• 3．如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（　　）

  A．AB=2BF	B．∠ACE= 1 2 ∠ACB
  C．AE=BE	D．CD⊥BE
  组卷：12129引用：75难度：0.9

  解析

• 4．具备下列条件的△ABC中，不是直角三角形的是（　　）

  A．∠A+∠B=∠C	B．∠A-∠B=∠C
  C．∠A：∠B：∠C=1：2：3	D．∠A=∠B=3∠C
  组卷：13681引用：104难度：0.9

  解析

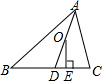• 5．如图，AD是△ABC的角平分线，点O在AD上，且OE⊥BC于点E，∠BAC=60°，∠C=80°，则∠EOD的度数为（　　）

  A．20°

  B．30°

  C．10°

  D．15°
  组卷：3381引用：38难度：0.9

  解析

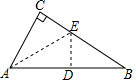• 6．如图，在Rt△ABC中，∠C=90°，沿过点A的一条直线AE折叠Rt△ABC，使点C恰好落在AB边的中点D处，则∠B的度数是（　　）

  A．25°

  B．30°

  C．40°

  D．45°
  组卷：315引用：6难度：0.7

  解析

• 7．一个三角形的两边长分别是3和7，且第三边长为整数，这样的三角形周长最大的值为（　　）

  A．15

  B．16

  C．18

  D．19
  组卷：574引用：17难度：0.9

  解析

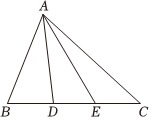• 8．如图，在△ABC中，D，E分别为BC上两点，且BD=DE=EC，则图中面积相等的三角形有（　　）对．

  A．4

  B．5

  C．6
  组卷：11引用：1难度：0.5

  解析

三、解答题（共八题：共66分）

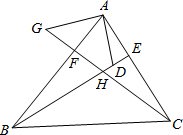• 25．如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．试猜想线段AD与AG的数量及位置关系，并证明你的猜想．
  组卷：333引用：7难度：0.5

  解析

• 26．（1）已知，如图①，在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为点D、E，求证：DE=BD+CE．
  （2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意钝角，请问结论DE=BD+CE是否成立？若成立，请你给出证明；若不成立，请说明理由．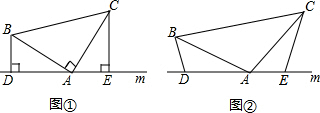
  
  组卷：10541引用：47难度：0.5

  解析