2022-2023学年山西省运城市八年级（上）期中数学试卷
发布：2024/8/31 8:0:8
一、选择题（本题共10个小题，每小题3分，共30分，请将每题中唯一正确答案的
-
1．
的相反数是（ ）3组卷：874引用：27难度：0.9 -
2．在实数
，-5，π2，4，3.14159，227，0.2323323332…（每相邻两个2之间依次多一个3）中，无理数有（ ）38组卷：173引用：4难度：0.8 -
3．河东池盐业博物馆位于运城市盐湖区盐池的北岸，当地人习惯称之为“池神庙”．它也是我国惟一保存良好的盐神庙．站在池神庙高处俯瞰，“千古中条一池雪”的诗景美不胜收．如图是河东池盐业博物馆的平面图，已知池神庙的位置是（0，0），老火车遗址的位置是（-6，2），则盐湖生态公园的位置是（ ）组卷：5引用：2难度：0.6 -
4．下列计算中，正确的是（ ）
组卷：209引用：7难度：0.9 -
5．全红婵在出征2022年国际泳联跳水世界杯前刻苦进行跳水训练，教练对她20次的训练成绩进行统计分析，判断她的成绩是否稳定，则教练需要知道全红婵这20次成绩的（ ）
组卷：5引用：2难度：0.5 -
6．法国数学家笛卡尔（Descartes,1596-1650），最早引入平面直角坐标系，用代数方法研究几何，这种研究方法体现的数学思想是（ ）组卷：16引用：1难度：0.8 -
7．在平面直角坐标系中，下列说法正确的是（ ）
组卷：31引用：2难度：0.6
三、解答题（本大题共8个小题，共70分）
-
22．综合与实践
【背景介绍】勾股定理是几何学中的明珠，充满着魅力．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是大正方形的面积有两种求法，一种是等于c2，另一种是等于四个直角三角形与一个小正方形的面积之和，即，从而得到等式12ab×4+（b-a）2，化简便得结论a2+b2=c2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．c2=12ab×4+（b-a）2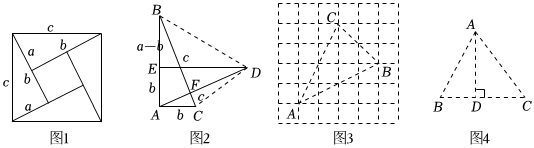
【方法运用】千百年来，人们对勾股定理的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在2010年构造发现了一个新的证法：把两个全等的直角△ABC和△DEA如图2放置，其三边长分别为a,b,c,∠BAC=∠DEA=90°，显然BC⊥AD．
（1）请用a,b,c分别表示出四边形ABDC，梯形AEDC，△EBD的面积，再探究这三个图形面积之间的关系，证明勾股定理a2+b2=c2．
（2）【方法迁移】请利用“双求法”解决下面的问题：如图3，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则AB边上的高为 ．
（3）如图4，在△ABC中，AD是BC边上的高，AB=4，AC=5，BC=6，设BD=x,求x的值．组卷：1164引用：9难度：0.5 -
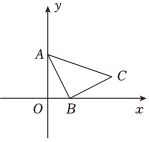23．综合与探究：如图，在平面直角坐标系中，已知A（0，a），B（b,0），其中a,b满足，点C是第一象限内的点，∠ABC=90°，AB=BC．|a-2|+（b-1）2=0
（1）分别求出点A、B、C的坐标．
（2）如果在第二象限内有一点P（m,1），是否存在点P，使得△ABP的面积等于△ABC的面积？若存在，请求出点P的坐标；若不存在，说明理由．
（3）在平面直角坐标系是否存在点E，使△ABE与△ABC全等，若存在，请直接写出点E的坐标；若不存在，请说明理由．组卷：88引用：2难度：0.2
