2023-2024学年湖南省郴州九中九年级（上）第一次月考数学试卷

一.选择题（共10小题，每小题0分）

• 1．如图，菱形ABCD中，AC=8．BD=6．则菱形的面积为（　　）

  A．20

  B．40

  C．28

  D．24
  组卷：534引用：7难度：0.8

  解析

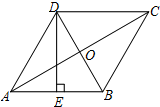• 2．如图，菱形ABCD的对角线AC、BD相交于点O，DE⊥AB于点E，若AB=5，DE=4，则在下列结论中正确的是（　　）

  A．DB=5

  B．AE=4

  C．BE=2

  D．OA=3 2
  组卷：507引用：6难度：0.8

  解析

• 3．▱ABCD中，AC，BD是两条对角线，如果添加一个条件，可推出▱ABCD是菱形，那么这个条件可以是（　　）

  A．AB=CD

  B．AC=BD

  C．AC⊥BD

  D．AB⊥BD
  组卷：2571引用：13难度：0.8

  解析

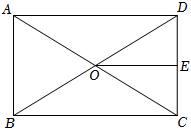• 4．如图，矩形ABCD的对角线AC、BD相交于点O，点E是CD的中点，若OE=3，则BC的长为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：2146引用：14难度：0.8

  解析

• 5．下列说法正确的是（　　）

  A．对角线相等的四边形是矩形

  B．对角线互相垂直且相等的四边形是正方形

  C．对角线互相垂直平分的四边形是菱形

  D．四边相等的四边形是正方形
  组卷：189引用：7难度：0.5

  解析

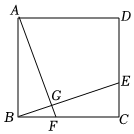• 6．如图，E、F分别是正方形ABCD的边CD、BC上的点，且CE=BF，AF、BE相交于点G，下列结论中正确的是（　　）
  ①AF=BE；
  ②AF⊥BE；
  ③AG=GE；
  ④S_△ABG=S_{四边形CEGF}．

  A．①②③

  B．①②④

  C．①③④

  D．②③④
  组卷：835引用：6难度：0.8

  解析

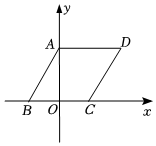• 7．如图，在平面直角坐标系中，菱形ABCD的顶点A，B，C在坐标轴上，若点A、B的坐标分别为（0，2）、（-1，0），则点D的坐标为（　　）

  A．（ 5 ，2）

  B．（2， 5 ）

  C．（ 3 ，2）

  D．（2， 3 ）
  组卷：494引用：9难度：0.7

  解析

三.解答题（共8小题）

• 22．如图，已知四边形ABCD为正方形，AB=3

  2

  ，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
  （1）求证：矩形DEFG是正方形；
  （2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
  组卷：10255引用：14难度：0.3

  解析

• 23．小明学习了特殊的四边形后，对特殊四边形的探究产生了兴趣，发现另外一类特殊四边形，如图1，我们把两条对角线互相垂直的四边形叫做垂美四边形．
  
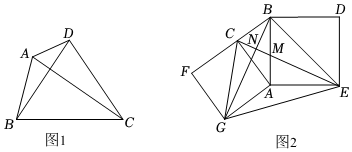
  （1）概念理解：在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是

  ．
  （2）性质探究：通过探究，直接写出垂美四边形ABCD的面积S与两条对角线AC、BD之间的数量关系：

  ．
  （3）问题解决：如图2，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结BG、CE交于点N，CE交AB于点M，连结GE．
  ①求证：四边形BCGE为垂美四边形；
  ②已知AC=4，AB=5，则四边形BCGE的面积为

  ．
  组卷：268引用：4难度：0.4

  解析