菁于教，优于学

申请校本题库

试卷征集

加入会员

操作视频

当前位置：试卷中心 > 试卷详情

2022-2023学年山东省济宁市任城区八年级（下）期中数学试卷（五四学制）

发布：2024/6/2 8:0:8

一、单选题（本大题满分30分，每小题3分.每小题只有一个符合题意的选项，请你将正确选项的代号填在答题卡）

1．下列二次根式中，是最简二次根式的是（　　）
A．
8
B．
2
C．
1
3
D．
9
组卷：115引用：4难度：0.8
解析
2．正方形具有而菱形不一定具有的性质是（　　）
A．对角线相等 B．对角线互相垂直且平分
C．四条边都相等 D．对角线平分一组对角
组卷：293引用：9难度：0.7
解析
3．一元二次方程x²-16=0的根是（　　）
A．x=2 B．x=4 C．x₁=2，x₂=-2 D．x₁=4，x₂=-4
组卷：958引用：10难度：0.9
解析
4．代数式
x
-
5
x
-
6
有意义，则x的取值范围是（　　）
A．x≤5 B．x≥5 C．x＞5且x≠6 D．x≥5且x≠6
组卷：775引用：7难度：0.9
解析
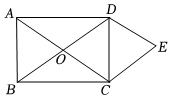5．如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD，已知AB=6cm,BC=8cm,则四边形ODEC的周长为（　　）
A．10cm B．12cm C．16cm D．20cm
组卷：105引用：3难度：0.5
解析
6．下列各式计算正确的是（　　）
A．
3
3
-
2
3
=
1
B．
（
-
3
）
2
=
-
3
C．
3
+
2
=
5
D．
（
5
+
3
）
（
5
-
3
）
=2
组卷：187引用：7难度：0.7
解析
7．用配方法解方程x²+8x+7=0，则配方正确的是（　　）
A．（x+4）²=9 B．（x-4）²=9 C．（x-8）²=16 D．（x+8）²=57
组卷：5853引用：188难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共55分）

22．阅读下面的材料，解决问题：
像
（
5
+
2
）
（
5
-
2
）
=
1
、
a
⋅
a
=
a
（
a
≥
0
）
、
（
b
+
1
）
（
b
-
1
）
=
b
-
1
（
b
≥
0
）
、……，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式．例如，
3
和
3
、
2
+
1
与
2
-
1
、
2
3
+
3
5
与
2
3
-
3
5
等都是互为有理化因式．在进行二次根式计算时，利用有理化因式，可以化去分母中的根号．我们把通过适当的变形化去分母中根号的运算叫做分母有理化．
例如：
1
2
3
=
3
2
3
×
3
=
3
6
；
2
+
1
2
-
1
=
（
2
+
1
）
2
（
2
-
1
）
（
2
+
1
）
=
2
+
2
2
+
1
2
-
1
=
3
+
2
2
；
（1）计算：
1
2
=
；
3
-
1
3
+
1
=
；
（2）计算：
1
1
+
2
+
1
2
+
3
+
1
3
+
4
+
……
+
1
2021
+
2022
+
1
2022
+
2023
；
（3）比较
15
-
14
和
14
-
13
的大小，并说明理由．
组卷：194引用：2难度：0.5
解析
23．问题解决：如图1，在矩形ABCD中，点E，F分别在AB，BC边上，DE=AF，DE⊥AF于点G．

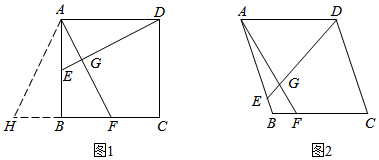
（1）求证：四边形ABCD是正方形；
（2）延长CB到点H，使得BH=AE，判断△AHF的形状，并说明理由．
类比迁移：如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE=AF，∠AED=60°，AE=6，BF=2，求DE的长．
组卷：3283引用：24难度：0.3
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

商务合作服务条款走进菁优

帮助中心兼职招聘意见反馈

深圳市菁优智慧教育股份有限公司

粤ICP备10006842号公网安备44030502001846号

©2010-2025 jyeoo.com 版权所有

深圳市市场监管
主体身份认证

APP开发者：深圳市菁优智慧教育股份有限公司| 应用名称：菁优网 | 应用版本：5.0.7 |隐私协议|第三方SDK|用户服务条款

广播电视节目制作经营许可证|出版物经营许可证|网站地图

本网部分资源来源于会员上传，除本网组织的资源外，版权归原作者所有，如有侵犯版权，请立刻和本网联系并提供证据，本网将在三个工作日内改正