2022-2023学年广东省江门市广州大学台山附中八年级（上）期中数学试卷
发布：2024/9/24 7:0:8
一、选择團（本大题共10小题，每小题3分，共30分）
-
1．下列各组数中，能作为一个三角形三边边长的是（ ）
组卷：3187引用：61难度：0.9 -
2．甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（ ）
组卷：2386引用：112难度：0.9 -
3．下列四个图形中，线段BE是△ABC的高的是（ ）
组卷：10970引用：168难度：0.9 -
4．如图，把平板电脑放在一个支架上面，就可以非常方便的使用它上网课，这样做的数学道理是（ ）组卷：304引用：14难度：0.6 -
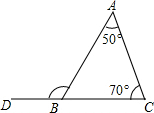5．如图，在△ABC中，∠A=50°，∠C=70°，则外角∠ABD的度数是（ ）组卷：5545引用：105难度：0.9 -
6．已知一个多边形的内角和为1080°，则这个多边形是（ ）
组卷：1975引用：31难度：0.9 -
7．下列说法不正确的是（ ）
组卷：1655引用：11难度：0.7
五、解答题（三）（本大题共2小题，每题12分，共24分）
-
22．等面积法是一种常用的、重要的数学解题方法．
（1）如图1，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB=5，CD⊥AB，则CD长为 ；
（2）如图2，在△ABC中，AB=4，BC=2，则△ABC的高CD与AE的比是 ；
（3）如图3，在△ABC中，∠C=90°（∠A＜∠ABC），点D，P分别在边AB，AC上，且BP=AP，DE⊥BP，DF⊥AP，垂足分别为点E，F．若BC=5，求DE+DF的值．组卷：1109引用：6难度：0.5 -
23．（1）如图①，在四边形ABCD中，AB=AD，∠B=∠ADC=90°．E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．小王同学探究此问题的方法：延长FD到点G，使DG=BE．连接AG．先证明△ABE≌△ADG，再证△AEF≌△AGF，可得出结论，他的结论应是 ．
【灵活运用】
（2）如图②，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立？请说明理由．
【延伸拓展】
（3）如图③，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD．若点E在CB的延长线上，点F在CD的延长线上，仍然满足EF=BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．
组卷：154引用：9难度：0.1
